Giới thiệu về Broadcasting¶
Nhớ rằng đối với các mảng có cùng kích thước, các phép toán nhị phân được thực hiện trên cơ sở từng phần tử:
import numpy as np
a = np.array([0, 1, 2]) b = np.array([5, 5, 5])a + b
array([5, 6, 7])
Broadcasting cho phép thực hiện các phép toán nhị phân trên các mảng có kích thước khác nhau – ví dụ, chúng ta có thể dễ dàng cộng một số nhalar (hãy nghĩ về một mảng có kích thước không) cho một mảng:
a + 5
array([5, 6, 7])
Chúng ta có thể coi đây là một phép toán mà nó kéo dãn hoặc nhân bản giá trị 5 vào mảng [5, 5, 5] và cộng các kết quả lại.
Chúng ta cũng có thể mở rộng điều này cho các mảng có số chiều cao hơn. Hãy quan sát kết quả khi chúng ta thêm một mảng một chiều vào một mảng hai chiều:
M = np.ones((3, 3))M
array([[ 1., 1., 1.], [ 1., 1., 1.], [ 1., 1., 1.]])
M + a
array([[ 1., 2., 3.], [ 1., 2., 3.], [ 1., 2., 3.]])
Ở đây, mảng một chiều a được kéo dài, hoặc phát sóng qua chiều thứ hai để phù hợp với hình dạng của M.
Mặc dù các ví dụ này tương đối dễ hiểu, nhưng các trường hợp phức tạp hơn có thể liên quan đến việc truyền phát của cả hai mảng. Hãy xem xét ví dụ sau:
a = np.arange(3)b = np.arange(3)[:, np.newaxis]print(a)print(b)
[0 1 2][[0] [1] [2]]
a + b
array([[0, 1, 2], [1, 2, 3], [2, 3, 4]])
Giống như trước đây chúng ta đã kéo dài hoặc phát sóng một giá trị để phù hợp với hình dạng của giá trị khác, ở đây chúng ta đã kéo dài cả a và b để phù hợp với một hình dạng chung, và kết quả là một mảng hai chiều!Hình học của những ví dụ này được minh họa trong hình vẽ sau (Mã để tạo ra biểu đồ này có thể được tìm thấy trong phần phụ lục, được điều chỉnh từ nguồn được xuất bản trong tài liệu astroML. Được sử dụng với sự cho phép).
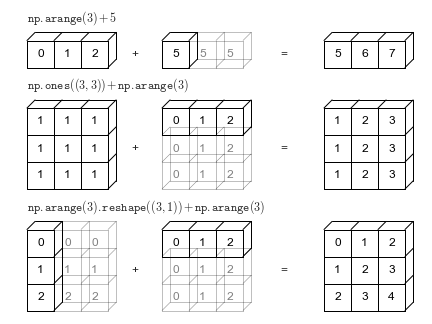
Các hộp ánh sáng đại diện cho các giá trị đã được phát sóng: một lần nữa, bộ nhớ bổ sung này thực ra không được cấp phát trong quá trình thực thi, nhưng nó có thể hữu ích trong việc hình dung rằng nó đã được cấp phát.
Quy tắc phát sóng¶
Truyền phát trong NumPy tuân theo một tập hợp nghiêm ngặt các quy tắc để xác định sự tương tác giữa hai mảng:
- Quy tắc 1: Nếu hai mảng khác nhau về số chiều, kích thước của mảng có số chiều ít hơn sẽ được thêm vào các giá trị 1 ở phía đầu (bên trái).
- Quy tắc 2: Nếu kích thước của hai mảng không khớp ở bất kỳ chiều nào, mảng có kích thước bằng 1 trong chiều đó sẽ được kéo dài để khớp với kích thước của mảng khác.
- Quy tắc 3: Nếu kích thước không khớp ở bất kỳ chiều nào và cả hai đều không bằng 1, một lỗi sẽ được báo.
Để làm rõ các quy tắc này, hãy xem xét một số ví dụ cụ thể.
Ví dụ phát sóng 1¶
Hãy xem cách thêm một mảng hai chiều vào một mảng một chiều:
M = np.ones((2, 3))a = np.arange(3)
Hãy xem xét một hoạt động trên hai mảng này. Cấu trúc của các mảng là
M.hình dạng = (2, 3)a.hình dạng = (3,)
Theo quy tắc 1, chúng ta thấy mảng a có số chiều ít hơn, vì vậy chúng ta sẽ thêm các giá trị 1 vào bên trái của nó:
M.shape -> (2, 3)a.shape -> (1, 3)
Theo quy tắc thứ 2, chúng ta thấy rằng chiều đầu tiên không đồng ý, vì vậy chúng ta kéo dài chiều này để phù hợp:
M.kích thước -> (2, 3)a.kích thước -> (2, 3)
Các hình khớp nhau, và chúng ta thấy rằng hình cuối cùng sẽ là (2, 3):
M + a
array([[ 1., 2., 3.], [ 1., 2., 3.]])
Ví dụ về phát thanh 2¶
Hãy xem một ví dụ trong đó cả hai mảng đều cần được phát sóng:
a = np.arange(3).reshape((3, 1))b = np.arange(3)
Một lần nữa, chúng ta sẽ bắt đầu bằng cách viết ra hình dạng của các mảng:
a.shape = (3, 1)b.shape = (3,)
Quy tắc 1 cho biết chúng ta phải thêm đệm vào hình dạng của b với số 1:
a.shape -> (3, 1)b.shape -> (1, 3)
Và quy tắc 2 cho chúng ta biết rằng chúng ta nâng cấp từng phần tử của danh sách này để phù hợp với kích thước tương ứng của mảng khác:
a.shape -> (3, 3)b.shape -> (3, 3)
Bởi vì kết quả phù hợp, những hình dạng này tương thích. Chúng ta có thể thấy điều này ở đây:
a + b
array([[0, 1, 2], [1, 2, 3], [2, 3, 4]])
Ví dụ về phát sóng 3¶
Bây giờ chúng ta hãy xem một ví dụ trong đó hai mảng không tương thích:
M = np.ones((3, 2))a = np.arange(3)
Đây chỉ là một tình huống khác một chút so với ví dụ đầu tiên: ma trận M đã được chuyển vị.
M.hình_dạng = (3, 2)a.hình_dạng = (3,)
Một lần nữa, quy tắc 1 cho chúng ta biết rằng chúng ta phải lót hình dạng của a bằng các số một:
M.shape -> (3, 2)a.shape -> (1, 3)
Theo quy tắc 2, chiều đầu tiên của a được kéo dãn để phù hợp với chiều của M:
M.hình dạng -> (3, 2)a.hình dạng -> (3, 3)
Bây giờ chúng ta tiến hành quy tắc 3 – hai hình dạng cuối cùng không khớp nhau, do đó hai mảng này không tương thích, như chúng ta có thể quan sát thông qua việc thực hiện phép toán này:
M + a
---------------------------------------------------------------------------ValueError Traceback (most recent call last)<ipython-input-13-9e16e9f98da6> in <module>()----> 1 M + aValueError: operands could not be broadcast together with shapes (3,2) (3,)
Lưu ý sự nhầm lẫn tiềm năng ở đây: bạn có thể tưởng tượng việc làm cho a và M tương thích bằng cách thêm khoảng cách vào hình dạng của a từ bên phải thay vì từ bên trái.Nhưng đây không phải là cách làm của luật phát sóng!Loại linh hoạt đó có thể hữu ích trong một số trường hợp, nhưng nó sẽ dẫn đến các vùng mơ hồ tiềm năng.Nếu bạn muốn thêm khoảng trống vào phía bên phải, bạn có thể làm điều này một cách rõ ràng bằng cách thay đổi hình dạng của mảng (chúng tôi sẽ sử dụng từ khóa np.newaxis được giới thiệu trong Cơ bản về mảng NumPy):
a[:, np.newaxis].shape
(3, 1)
M + a[:, np.newaxis]
array([[ 1., 1.], [ 2., 2.], [ 3., 3.]])
Cũng lưu ý rằng trong khi chúng ta đã tập trung vào toán tử + ở đây, các quy tắc phát sóng này áp dụng cho bất kỳ hàm nhị phân ufunc nào.Ví dụ, đây là hàm logaddexp(a, b), nó tính toán log(exp(a) + exp(b)) với độ chính xác cao hơn cách tiếp cận đơn giản:
np.logaddexp(M, a[:, np.newaxis])
array([[ 1.31326169, 1.31326169], [ 1.69314718, 1.69314718], [ 2.31326169, 2.31326169]])
Để biết thêm thông tin về các hàm toàn cục có sẵn, hãy tham khảo Computation on NumPy Arrays: Universal Functions.
Phát sóng trong thực tế¶
Hoạt động phát sóng (Broadcasting operations) là thành phần cốt lõi của nhiều ví dụ mà chúng ta sẽ thấy trong cuốn sách này. Bây giờ chúng ta sẽ xem một vài ví dụ đơn giản về cách chúng có thể hữu ích.
Căn giữa một mảng¶
Trong phần trước, chúng ta đã thấy rằng ufuncs cho phép người dùng NumPy loại bỏ nhu cầu viết các vòng lặp Python chậm chạp theo cách tường minh. Broadcasting mở rộng khả năng này.Một ví dụ thường thấy là khi căn giữa một mảng dữ liệu.Hãy tưởng tượng bạn có một mảng gồm 10 quan sát, mỗi quan sát gồm 3 giá trị.Sử dụng quy ước tiêu chuẩn (xem Biểu diễn dữ liệu trong Scikit-Learn), chúng ta sẽ lưu trữ điều này trong một mảng có kích thước $10 \times 3$:
X = np.random.random((10, 3))
Chúng ta có thể tính giá trị trung bình của mỗi đặc trưng bằng cách sử dụng phép gom nhóm mean trên chiều đầu tiên:
Xmean = X.mean(0)Xmean
array([ 0.53514715, 0.66567217, 0.44385899])
Và bây giờ chúng ta có thể căn giữa mảng X bằng cách trừ đi giá trị trung bình (đây là một phép toán phát sóng):
X_centered = X - Xmean
Để kiểm tra xem chúng ta đã thực hiện điều này đúng hay không, chúng ta có thể kiểm tra xem mảng được căn giữa có trung bình gần bằng không hay không:
X_centered.mean(0)
array([ 2.22044605e-17, -7.77156117e-17, -1.66533454e-17])
Đến trong kết đoạn máy chính xác, trung bình giờ đây là không.
Vẽ đồ thị hàm hai chiều¶
Một ứng dụng rất hữu ích của việc truyền phát dữ liệu là hiển thị hình ảnh dựa trên hàm hai chiều.Nếu chúng ta muốn định nghĩa một hàm $z = f(x, y)$, việc truyền phát dữ liệu có thể được sử dụng để tính toán hàm trên khung lưới:
# x and y have 50 steps from 0 to 5x = np.linspace(0, 5, 50)y = np.linspace(0, 5, 50)[:, np.newaxis]z = np.sin(x) ** 10 + np.cos(10 + y * x) * np.cos(x)
Chúng tôi sẽ sử dụng Matplotlib để vẽ biểu đồ cho mảng hai chiều này (các công cụ này sẽ được thảo luận chi tiết trong trang Biểu đồ Mật độ và Biểu đồ Đường viền):
%matplotlib inlineimport matplotlib.pyplot as plt
plt.imshow(z, origin='lower', extent=[0, 5, 0, 5], cmap='viridis')plt.colorbar();
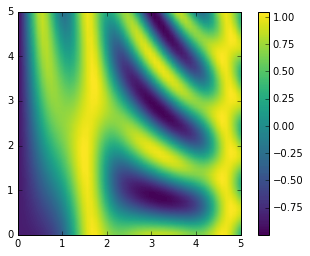
Kết quả là một biểu đồ hấp dẫn của hàm hai chiều.









