Khám phá Fancy Indexing¶
Chỉ số phức tạp đơn giản từ khái niệm: nó có nghĩa là chúng ta truyền một mảng chỉ số để truy cập nhiều phần tử trong mảng cùng một lúc.Ví dụ, xem xét mảng sau đây:
import numpy as np rand = np.random.RandomState(42) x = rand.randint(100, size=10) print(x)
[51 92 14 71 60 20 82 86 74 74]
Giả sử chúng ta muốn truy cập ba phần tử khác nhau. Chúng ta có thể làm như sau:
[x[3], x[7], x[2]]
[71, 86, 14]
Hoặc chúng ta có thể truyền một danh sách hoặc mảng duy nhất các chỉ số để có được kết quả tương tự:
ind = [3, 7, 4] x[ind]
array([71, 86, 60])
Khi sử dụng chỉ mục phức tạp, hình dạng của kết quả phản ánh hình dạng của các mảng chỉ mục thay vì hình dạng của mảng đang được chỉ mục:
ind = np.array([[3, 7], [4, 5]]) x[ind]
array([[71, 86], [60, 20]])
Chỉ số phức cũng hoạt động trong nhiều chiều. Hãy xem xét mảng sau đây:
X = np.arange(12).reshape((3, 4)) X
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
Tương tự như chỉ mục tiêu chuẩn, chỉ mục đầu tiên liên quan đến hàng, và chỉ mục thứ hai liên quan đến cột:
row = np.array([0, 1, 2]) col = np.array([2, 1, 3]) X[row, col]
array([ 2, 5, 11])
Lưu ý rằng giá trị đầu tiên trong kết quả là X[0, 2], thứ hai là X[1, 1], và thứ ba là X[2, 3].Việc kết hợp các chỉ số trong fancy indexing tuân theo tất cả các quy tắc broadcasting đã được đề cập trong Tính toán trên các mảng: Broadcasting.Vì vậy, ví dụ, nếu chúng ta kết hợp một vector cột và một vector hàng trong các chỉ số, chúng ta sẽ nhận được một kết quả hai chiều:
X[row[:, np.newaxis], col]
array([[ 2, 1, 3], [ 6, 5, 7], [10, 9, 11]])
Tại đây, mỗi giá trị hàng được kết hợp với mỗi vector cột, chính xác như chúng ta đã thấy trong quá trình phát sóng của các phép toán số học.Ví dụ:
row[:, np.newaxis] * col
array([[0, 0, 0], [2, 1, 3], [4, 2, 6]])
Luôn luôn quan trọng để nhớ rằng với các chỉ mục phức tạp, giá trị trả về phản ánh hình dạng được truyền tin của các chỉ mục, thay vì hình dạng của mảng đang được chỉ mục.
Tổ hợp chỉ mục¶
Để thực hiện các hoạt động mạnh mẽ hơn, chỉ mục phức tạp có thể kết hợp với các kế hoạch chỉ mục khác chúng ta đã thấy:
print(X)
[[ 0 1 2 3] [ 4 5 6 7] [ 8 9 10 11]]
Chúng ta có thể kết hợp các chỉ số phức tạp và đơn giản:
X[2, [2, 0, 1]]
array([10, 8, 9])
Chúng ta cũng có thể kết hợp chỉ số phức tạp với cắt (slicing):
X[1:, [2, 0, 1]]
array([[ 6, 4, 5],
[10, 8, 9]])
Và chúng ta có thể kết hợp chỉ mục phức tạp với việc áp dụng mặt nạ:
mask = np.array([1, 0, 1, 0], dtype=bool) X[row[:, np.newaxis], mask]
array([[ 0, 2],
[ 4, 6],
[ 8, 10]])
Tất cả các tùy chọn chỉ mục này kết hợp lại dẫn đến một tập hợp rất linh hoạt các hoạt động để truy cập và sửa đổi giá trị mảng.
Ví dụ: Chọn ngẫu nhiên các điểm¶
Một ứng dụng phổ biến của chỉ mục phức tạp là lựa chọn các phần con của các hàng từ ma trận. Ví dụ, chúng ta có thể có một ma trận $N$ x $D$ đại diện cho $N$ điểm trong $D$ chiều, như các điểm sau được vẽ từ một phân phối chuẩn hai chiều:
mean = [0, 0] cov = [[1, 2], [2, 5]] X = rand.multivariate_normal(mean, cov, 100) X.shape
(100, 2)
Sử dụng các công cụ vẽ biểu đồ mà chúng ta sẽ thảo luận trong Giới thiệu về Matplotlib, chúng ta có thể trực quan hóa các điểm này dưới dạng đồ thị phân tán:
%matplotlib inline import matplotlib.pyplot as plt import seaborn; seaborn.set() # for plot styling plt.scatter(X[:, 0], X[:, 1]);
Hãy sử dụng chỉ mục đặc biệt để chọn ngẫu nhiên 20 điểm. Chúng tôi sẽ làm điều này bằng cách trước tiên chọn ngẫu nhiên 20 chỉ mục không trùng lặp và sử dụng các chỉ mục này để chọn một phần của mảng gốc:
indices = np.random.choice(X.shape[0], 20, replace=False) indices
array([93, 45, 73, 81, 50, 10, 98, 94, 4, 64, 65, 89, 47, 84, 82, 80, 25, 90, 63, 20])
selection = X[indices] # fancy indexing hereselection.shape
(20, 2)
Bây giờ để xem những điểm đã được chọn, hãy vẽ các hình tròn lớn lên vị trí của các điểm được chọn:
plt.scatter(X[:, 0], X[:, 1], alpha=0.3) plt.scatter(selection[:, 0], selection[:, 1], facecolor='none', s=200);
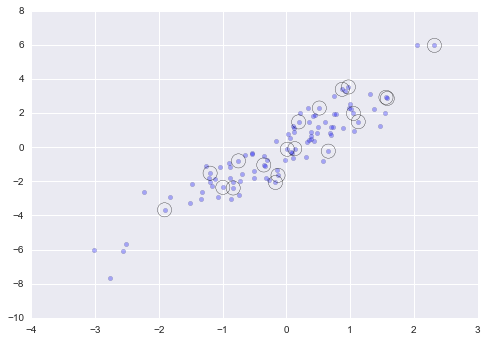
Kiểu chiến lược này thường được sử dụng để phân chia nhanh các tập dữ liệu, như thường được sử dụng trong việc chia thành tập huấn luyện/kiểm tra để xác thực các mô hình thống kê (xem Các thông số tùy chỉnh và Xác thực mô hình), và trong các phương pháp mẫu để trả lời các câu hỏi thống kê.
Sửa đổi giá trị với Fhay Indexing¶
Tương tự như việc sử dụng chỉ số phức để truy cập các phần tử của một mảng, chúng cũng có thể được sử dụng để sửa đổi các phần tử của một mảng.Ví dụ, hãy tưởng tượng chúng ta có một mảng các chỉ số và chúng ta muốn đặt các phần tử tương ứng trong một mảng thành một giá trị nào đó:
x = np.arange(10) i = np.array([2, 1, 8, 4]) x[i] = 99 print(x)
[ 0 99 99 3 99 5 6 7 99 9]
Chúng ta có thể sử dụng bất kỳ toán tử gán nào cho việc này. Ví dụ như:
x[i] -= 10 print(x)
[ 0 89 89 3 89 5 6 7 89 9]
Lưu ý, tuy nhiên, rằng các chỉ số lặp lại với những hoạt động này có thể gây ra một số kết quả không mong đợi. Hãy xem xét ví dụ sau:
x = np.zeros(10) x[[0, 0]] = [4, 6] print(x)
[ 6. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
Chỗ nào mất số 4 rồi? Kết quả của phép thao tác này là trước tiên gán x[0] = 4, theo sau là x[0] = 6.Kết quả, đương nhiên, là x[0] chứa giá trị 6.
Đủ công bằng, nhưng hãy xem xét hoạt động này:
i = [2, 3, 3, 4, 4, 4] x[i] += 1 x
array([ 6., 0., 1., 1., 1., 0., 0., 0., 0., 0.])
Bạn có thể mong đợi rằng x[3] sẽ chứa giá trị 2 và x[4] sẽ chứa giá trị 3, vì đây là số lần mà mỗi chỉ số được lặp lại. Tại sao điều này không xảy ra?Về mặt ý tưởng, điều này xảy ra vì x[i] += 1 được hiểu là một cách viết tắt của x[i] = x[i] + 1. x[i] + 1 được đánh giá và sau đó kết quả được gán vào các chỉ số trong x.Với điều này trong đầu, không phải là việc gia tăng xảy ra nhiều lần, mà là việc gán, dẫn đến các kết quả khá khó hiểu.
Vậy thì nếu bạn muốn tình huống khác, nơi thao tác được lặp lại, bạn có thể sử dụng phương thức at() của các hàm ufuncs (có sẵn từ phiên bản NumPy 1.8) và thực hiện như sau:
x = np.zeros(10) np.add.at(x, i, 1) print(x)
[ 0. 0. 1. 2. 3. 0. 0. 0. 0. 0.]
Phương thức at() thực hiện việc áp dụng toán tử đã cho tại các chỉ số cụ thể (ở đây là i) với giá trị đã cho (ở đây là 1), ngay tại chỗ.Một phương thức khác tương tự trong tinh thần là phương thức reduceat() của ufuncs, mà bạn có thể đọc thêm trong tài liệu NumPy.
Ví dụ: Phân loại dữ liệu¶
Bạn có thể sử dụng những ý tưởng này để phân chia dữ liệu hiệu quả để tạo histogram bằng tay.Ví dụ, hãy tưởng tượng chúng ta có 1.000 giá trị và muốn nhanh chóng tìm xem chúng nằm ở đâu trong một mảng các bins.Chúng ta có thể tính toán điều này bằng cách sử dụng ufunc.at như sau:
np.random.seed(42) x = np.random.randn(100) # compute a histogram by hand bins = np.linspace(-5, 5, 20) counts = np.zeros_like(bins) # find the appropriate bin for each x i = np.searchsorted(bins, x) # add 1 to each of these bins np.add.at(counts, i, 1)
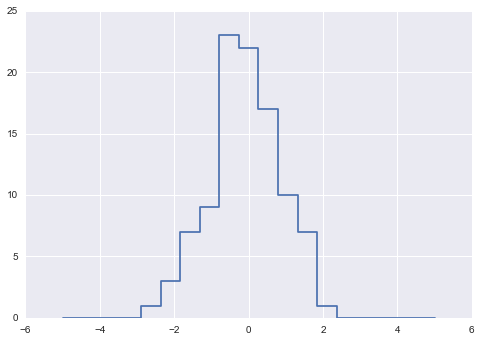
Số liệu hiện tại phản ánh số điểm trong mỗi khung – nghĩa là một biểu đồ tần số:
# plot the resultsplt.plot(bins, counts, linestyle='steps');
Tất nhiên, sẽ rất ngốc nếu phải làm điều này mỗi khi bạn muốn vẽ biểu đồ histogram.Đó là lý do vì sao Matplotlib cung cấp tính năng plt.hist(), giúp thực hiện cùng một việc này chỉ trong một dòng duy nhất:
plt.hist(x, bins, histtype='step');
Hàm này sẽ tạo ra một đồ thị gần như giống như đồ thị được thấy ở đây.Để tính các khoảng binning, matplotlib sử dụng hàm np.histogram, hàm này thực hiện một tính toán rất tương tự như chúng ta đã làm trước đó. Hãy so sánh hai cái ở đây:
print("NumPy routine:") %timeit counts, edges = np.histogram(x, bins) print("Custom routine:") %timeit np.add.at(counts, np.searchsorted(bins, x), 1)
NumPy routine:10000 loops, best of 3: 97.6 µs per loopCustom routine:10000 loops, best of 3: 19.5 µs per loop
Thuật toán một dòng duy nhất của chúng tôi nhanh hơn một số lần so với thuật toán tối ưu hóa trong NumPy! Làm thế nào điều này có thể?Nếu bạn khám phá mã nguồn của np.histogram (bạn có thể làm điều này trong IPython bằng cách gõ np.histogram??), bạn sẽ thấy rằng nó phức tạp hơn rất nhiều so với việc tìm kiếm và đếm đơn giản mà chúng tôi đã làm; điều này bởi vì thuật toán của NumPy linh hoạt hơn và đặc biệt được thiết kế để tăng hiệu suất khi số điểm dữ liệu trở nên lớn hơn:
x = np.random.randn(1000000)print("NumPy routine:")%timeit counts, edges = np.histogram(x, bins)print("Custom routine:")%timeit np.add.at(counts, np.searchsorted(bins, x), 1)
NumPy routine:10 loops, best of 3: 68.7 ms per loopCustom routine:10 loops, best of 3: 135 ms per loop
Điều mà so sánh này cho thấy là hiệu năng thuật toán hầu như không bao giờ là một câu hỏi đơn giản. Một thuật toán hiệu quả cho các bộ dữ liệu lớn sẽ không phải lúc nào cũng là sự lựa chọn tốt nhất cho các bộ dữ liệu nhỏ, và ngược lại (xem Big-O Notation).Nhưng lợi ích của việc viết thuật toán này bằng chính tay bạn là với kiến thức về các phương pháp cơ bản này, bạn có thể sử dụng các khối xây dựng này để mở rộng và thực hiện một số hành vi tùy chỉnh rất thú vị.Chìa khóa để sử dụng Python hiệu quả trong các ứng dụng dữ liệu là biết về các tiện ích chung như np.histogram và khi nào thì thích hợp sử dụng chúng, nhưng cũng biết cách sử dụng các chức năng cấp thấp hơn khi bạn cần hành vi cụ thể hơn.









