Khuyến khích GMM: Nhược điểm của k-Means¶
Hãy cùng nhìn vào một số điểm yếu của phương pháp k-means và suy nghĩ về cách cải tiến mô hình gom cụm.Như chúng ta đã thấy ở phần trước, với dữ liệu đơn giản, rời rạc, k-means tìm ra các kết quả gom cụm phù hợp.
Ví dụ, nếu chúng ta có các đoạn dữ liệu đơn giản, thuật toán k-means có thể nhanh chóng gán nhãn cho những cụm đó một cách gần giống với những gì chúng ta có thể làm bằng mắt:
# Generate some datafrom sklearn.datasets.samples_generator import make_blobsX, y_true = make_blobs(n_samples=400, centers=4, cluster_std=0.60, random_state=0)X = X[:, ::-1] # flip axes for better plotting
# Plot the data with K Means Labelsfrom sklearn.cluster import KMeanskmeans = KMeans(4, random_state=0)labels = kmeans.fit(X).predict(X)plt.scatter(X[:, 0], X[:, 1], c=labels, s=40, cmap='viridis');
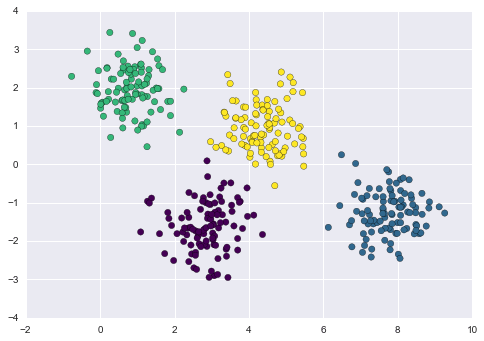
Từ một quan điểm trực quan, chúng ta có thể kỳ vọng rằng việc gán cụm cho một số điểm cụ thể sẽ chắc chắn hơn so với những điểm khác: ví dụ, có vẻ như có một chút chồng chéo giữa hai cụm ở giữa, điều này cho thấy chúng ta có thể không hoàn toàn tự tin trong việc gán cụm cho các điểm nằm giữa chúng.
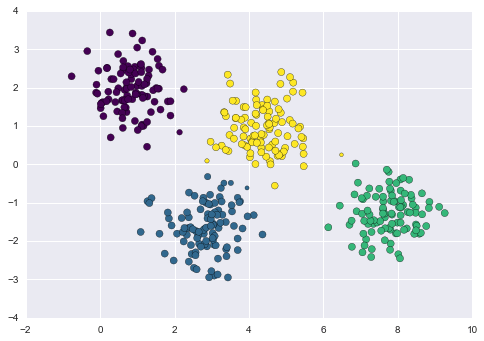
Một cách để hiểu về mô hình k-means là nó đặt một đường tròn (hoặc ở các chiều cao hơn, một siêu quả cầu) ở trung tâm của mỗi cụm, với bán kính được xác định bởi điểm xa nhất trong cụm.Bán kính này hoạt động như một giới hạn cứng cho việc gán cụm trong bộ huấn luyện: bất kỳ điểm ngoài đường tròn này đều không được coi là thành viên của cụm.Chúng ta có thể trực quan hóa mô hình cụm này bằng hàm sau:
from sklearn.cluster import KMeansfrom scipy.spatial.distance import cdistdef plot_kmeans(kmeans, X, n_clusters=4, rseed=0, ax=None): labels = kmeans.fit_predict(X) # plot the input data ax = ax or plt.gca() ax.axis('equal') ax.scatter(X[:, 0], X[:, 1], c=labels, s=40, cmap='viridis', zorder=2) # plot the representation of the KMeans model centers = kmeans.cluster_centers_ radii = [cdist(X[labels == i], [center]).max() for i, center in enumerate(centers)] for c, r in zip(centers, radii): ax.add_patch(plt.Circle(c, r, fc='#CCCCCC', lw=3, alpha=0.5, zorder=1))
kmeans = KMeans(n_clusters=4, random_state=0)plot_kmeans(kmeans, X)
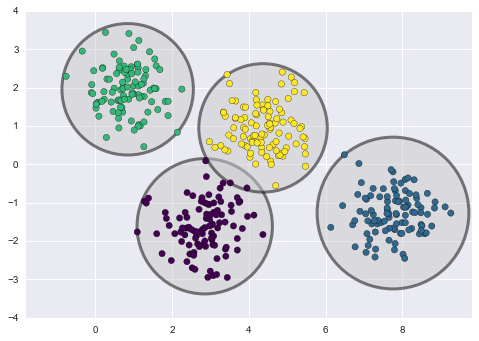
Một quan sát quan trọng cho k-means là các mô hình cụm này phải là hình tròn: k-means không có cách tích hợp để tính toán các cụm có hình dạng oval hoặc elliptical.Vì vậy, ví dụ, nếu chúng ta lấy cùng dữ liệu và biến đổi nó, phân công cụm sẽ trở nên mơ hồ:
rng = np.random.RandomState(13)X_stretched = np.dot(X, rng.randn(2, 2))kmeans = KMeans(n_clusters=4, random_state=0)plot_kmeans(kmeans, X_stretched)
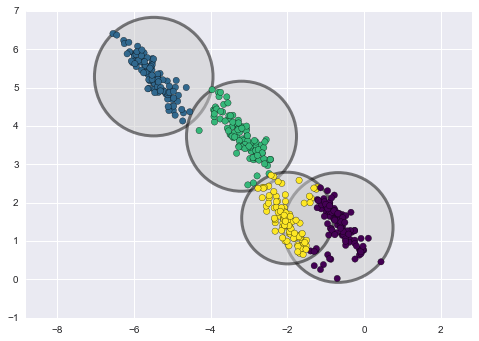
Theo cách mắt thường, chúng ta nhận ra rằng các nhóm được biến đổi này không phải là các hình tròn, và do đó các nhóm hình tròn sẽ không phù hợp.Tuy nhiên, phương pháp k-means không đủ linh hoạt để giải thích điều này, và cố gắng ép dữ liệu vào bốn nhóm hình tròn.Kết quả là việc gán nhãn nhóm bị trộn lẫn khi các hình tròn sau này chồng lên nhau: đặc biệt là phần dưới cùng bên phải của biểu đồ này.Có thể tưởng tượng giải quyết tình huống cụ thể này bằng cách tiền xử lý dữ liệu bằng phân tích thành phần chính (xem Sâu hơn về Phân tích thành phần chính), nhưng trong thực tế không có đảm bảo rằng việc thực hiện toàn bộ dữ liệu này sẽ làm hình tròn hóa dữ liệu cá nhân.
Hai nhược điểm của k-means — sự thiếu linh hoạt trong hình dạng cụm và sự thiếu phân loại xác suất cho cụm — có nghĩa là đối với nhiều tập dữ liệu (đặc biệt là tập dữ liệu chiều thấp), nó có thể không hoạt động tốt như bạn hy vọng.
Bạn có thể tưởng tượng cách khắc phục nhược điểm này bằng cách tổng quát hóa mô hình k-means: ví dụ, bạn có thể đo độ không chắc chắn trong việc gán cụm bằng cách so sánh khoảng cách từng điểm đến tất cả các tâm cụm, thay vì chỉ tập trung vào điểm gần nhất.Bạn cũng có thể hình dung về việc cho phép ranh giới của các cụm đồng thời là ellips, thay vì chỉ là các vòng tròn, để tính đến các cụm không có hình dạng hình tròn.Rất có thể điều này là hai thành phần cần thiết của một mô hình gom cụm khác, mô hình hỗn hợp Gaussian.
Tổng quát hóa E-M: Mô hình hỗn hợp Gaussian¶
Mô hình hỗn hợp Gaussian (GMM) cố gắng tìm một sự kết hợp của các phân phối xác suất Gaussian nhiều chiều mà mô hình tốt nhất bất kỳ tập dữ liệu đầu vào nào.Trong trường hợp đơn giản nhất, GMMs có thể được sử dụng để tìm các cụm theo cùng cách như k-means:
from sklearn.mixture import GMMgmm = GMM(n_components=4).fit(X)labels = gmm.predict(X)plt.scatter(X[:, 0], X[:, 1], c=labels, s=40, cmap='viridis');
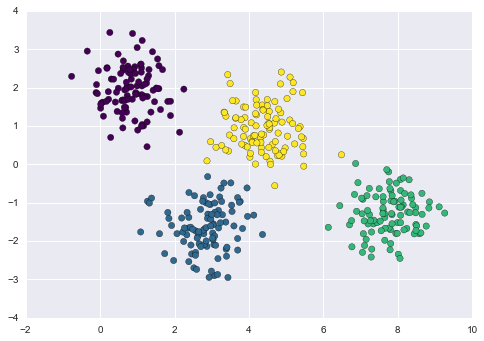
Tuy nhiên, vì GMM chứa một mô hình xác suất ẩn, nên cũng có thể tìm cách gán cụm theo xác suất – trong Scikit-Learn, điều này được thực hiện bằng cách sử dụng phương thức predict_proba.
probs = gmm.predict_proba(X)print(probs[:5].round(3))
[[ 0. 0. 0.475 0.525] [ 0. 1. 0. 0. ] [ 0. 1. 0. 0. ] [ 0. 0. 0. 1. ] [ 0. 1. 0. 0. ]]
Chúng ta có thể hình dung sự không chắc chắn này bằng cách làm cho kích thước mỗi điểm tỉ lệ với sự chắc chắn của dự đoán; nhìn vào hình vẽ sau đây, chúng ta có thể thấy rằng chính những điểm ở biên giữa các cụm chính là phản ánh sự không chắc chắn trong việc gán cụm:
size = 50 * probs.max(1) ** 2 # square emphasizes differencesplt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', s=size);
Dưới cái nắp, một mô hình hỗn hợp Gaussian rất tương tự với thuật toán k-means: nó sử dụng phương pháp expectation–maximization để làm các bước sau đây một cách định tính:
Chọn giá trị ban đầu cho vị trí và hình dạng
Lặp lại cho đến khi hội tụ:
- Bước E: đối với mỗi điểm, tìm các trọng số biểu diễn xác suất thuộc về từng nhóm
- Bước M: đối với mỗi nhóm, cập nhật vị trí, chuẩn hóa và hình dạng dựa trên tất cả các điểm dữ liệu, sử dụng các trọng số
Chọn các đoán đầu cho vị trí và hình dạng
Lặp lại cho đến khi hội tụ:
- Bước E: đối với mỗi điểm, tìm các trọng số mã hóa xác suất thuộc về mỗi cụm
- Bước M: đối với mỗi cụm, cập nhật vị trí, chuẩn hóa và hình dạng của cụm dựa trên tất cả các điểm dữ liệu, sử dụng các trọng số
Kết quả của việc này là mỗi cụm được liên kết không phải với một hình cầu cứng, mà là với mô hình Gaussian mềm.Giống như trong phương pháp mong đợi-tối đa k-means, thuật toán này đôi khi có thể bỏ qua giải pháp tối ưu toàn cầu và vì vậy trong thực tế, nhiều khởi tạo ngẫu nhiên khác nhau được sử dụng.
Hãy tạo một hàm giúp chúng ta biểu diễn các vị trí và hình dạng của các cụm GMM bằng cách vẽ các đường ellipse dựa trên kết quả của GMM:
from matplotlib.patches import Ellipsedef draw_ellipse(position, covariance, ax=None, **kwargs): """Draw an ellipse with a given position and covariance""" ax = ax or plt.gca() # Convert covariance to principal axes if covariance.shape == (2, 2): U, s, Vt = np.linalg.svd(covariance) angle = np.degrees(np.arctan2(U[1, 0], U[0, 0])) width, height = 2 * np.sqrt(s) else: angle = 0 width, height = 2 * np.sqrt(covariance) # Draw the Ellipse for nsig in range(1, 4): ax.add_patch(Ellipse(position, nsig * width, nsig * height, angle, **kwargs)) def plot_gmm(gmm, X, label=True, ax=None): ax = ax or plt.gca() labels = gmm.fit(X).predict(X) if label: ax.scatter(X[:, 0], X[:, 1], c=labels, s=40, cmap='viridis', zorder=2) else: ax.scatter(X[:, 0], X[:, 1], s=40, zorder=2) ax.axis('equal') w_factor = 0.2 / gmm.weights_.max() for pos, covar, w in zip(gmm.means_, gmm.covars_, gmm.weights_): draw_ellipse(pos, covar, alpha=w * w_factor)
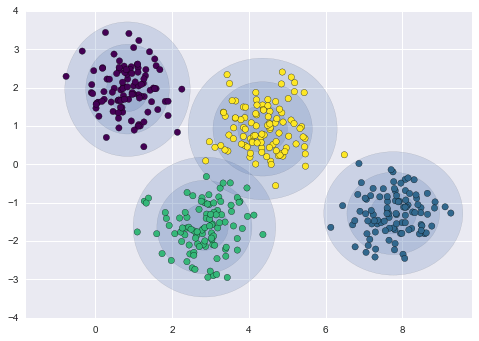
Với điều này, chúng ta có thể xem xét những gì mô hình GMM bốn thành phần mang lại cho dữ liệu ban đầu của chúng ta:
gmm = GMM(n_components=4, random_state=42)plot_gmm(gmm, X)
Tương tự, chúng ta có thể sử dụng phương pháp GMM để phù hợp với tập dữ liệu bị kéo dãn của chúng ta; cho phép mô hình có ma trận hiệp phương sai đầy đủ sẽ phù hợp ngay cả với những cụm dữ liệu có hình dạng dài và thon:
gmm = GMM(n_components=4, covariance_type='full', random_state=42)plot_gmm(gmm, X_stretched)
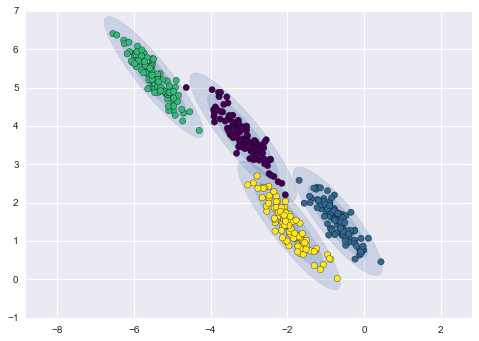
Điều này làm rõ rằng GMM giải quyết hai vấn đề thực tế chính với k-means đã gặp trước đây.
Chọn loại tương quan¶
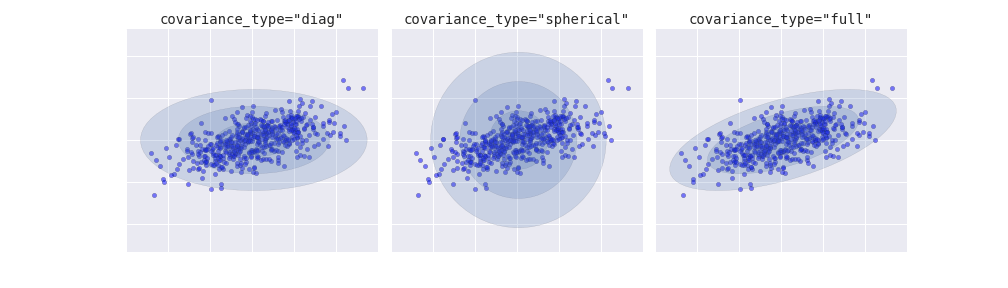
Nếu bạn xem chi tiết các phù hợp trước đó, bạn sẽ thấy rằng tùy chọn covariance_type được đặt khác nhau trong mỗi trường hợp.Tham số siêu này kiểm soát độ tự do trong hình dạng của mỗi cụm; việc thiết lập chính xác cho từng vấn đề cụ thể là rất quan trọng.Giá trị mặc định là covariance_type="diag", có nghĩa là kích thước của cụm trên mỗi chiều có thể được đặt độc lập, với hình elip kết quả bị ràng buộc sao cho song song với trục.Một mô hình đơn giản hơn và nhanh hơn một chút là covariance_type="spherical", hạn chế hình dạng của cụm sao cho tất cả các chiều bằng nhau. Cách phân cụm thu được sẽ có đặc điểm tương tự như phương pháp k-means, mặc dù không hoàn toàn tương đương.Một mô hình phức tạp và tốn thời gian tính toán hơn (đặc biệt là khi số chiều tăng lên) là sử dụng covariance_type="full", cho phép mô hình mỗi cụm được mô phỏng như một hình elip với hướng tùy ý.
Chúng ta có thể thấy một biểu đồ trực quan của ba lựa chọn này cho một nhóm cụm duy nhất trong hình sau:
GMM như Ước lượng Mật độ¶
Mặc dù GMM thường được phân loại là một thuật toán phân cụm, nhưng về bản chất, đó là một thuật toán cho ước lượng mật độ.
Như một ví dụ, hãy xem xét một số dữ liệu được tạo ra từ chức năng make_moons của Scikit-Learn, chúng ta đã thấy trong In Depth: Gom cụm K-Means:
from sklearn.datasets import make_moonsXmoon, ymoon = make_moons(200, noise=.05, random_state=0)plt.scatter(Xmoon[:, 0], Xmoon[:, 1]);
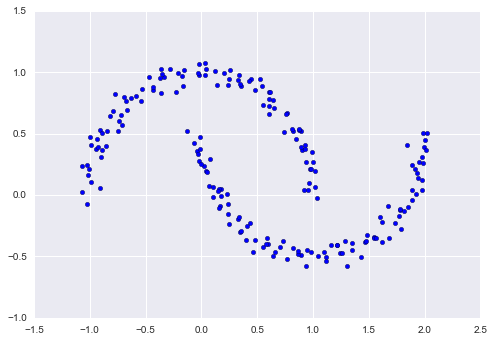
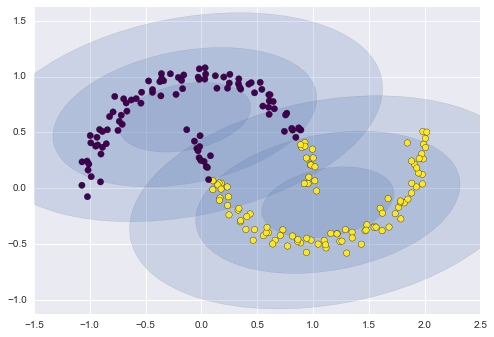
Nếu chúng ta cố gắng đưa điều này vào mô hình GMM hai thành phần nhìn như một mô hình gom cụm, kết quả không đặc biệt hữu ích:
gmm2 = GMM(n_components=2, covariance_type='full', random_state=0)plot_gmm(gmm2, Xmoon)
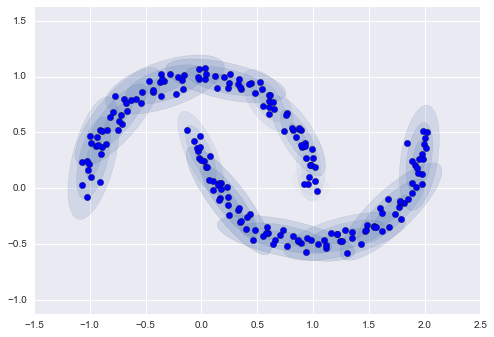
Tuy nhiên, nếu chúng ta sử dụng nhiều thành phần hơn và bỏ qua các nhãn cụm, chúng ta sẽ tìm được một sự khớp rất gần với dữ liệu đầu vào:
gmm16 = GMM(n_components=16, covariance_type='full', random_state=0)plot_gmm(gmm16, Xmoon, label=False)
Ở đây, sự kết hợp của 16 phân phối Gauss không phục vụ để tìm các cụm dữ liệu được tách rời, mà thay vào đó phục vụ mô hình hóa tổng quan của dữ liệu đầu vào.Đây là một mô hình sinh của phân phối, có nghĩa là GMM cung cấp cho chúng tôi công thức để tạo ra dữ liệu ngẫu nhiên mới có phân phối tương tự như dữ liệu đầu vào của chúng tôi.Ví dụ, đây là 400 điểm mới được vẽ từ phân phối GMM 16 thành phần này được phù hợp với dữ liệu ban đầu của chúng tôi:
Xnew = gmm16.sample(400, random_state=42)plt.scatter(Xnew[:, 0], Xnew[:, 1]);
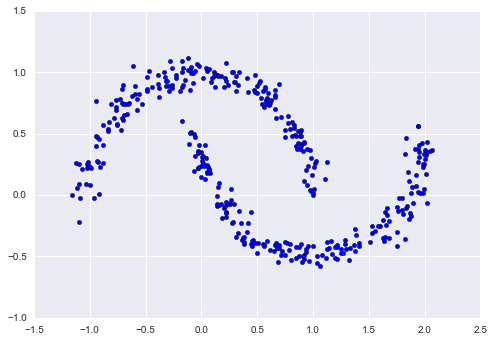
GMM rất tiện lợi như một phương pháp linh hoạt để mô hình hóa một phân phối đa chiều tùy ý của dữ liệu.
Bao nhiêu thành phần?¶
Thực tế là việc GMM là một mô hình sinh tử đưa cho chúng ta một phương pháp tự nhiên để xác định số thành phần tối ưu cho một tập dữ liệu cụ thể.
Hãy cùng nhìn vào AIC và BIC như là một hàm của số thành phần GMM cho tập dữ liệu mặt trăng của chúng ta:
n_components = np.arange(1, 21)models = [GMM(n, covariance_type='full', random_state=0).fit(Xmoon) for n in n_components]plt.plot(n_components, [m.bic(Xmoon) for m in models], label='BIC')plt.plot(n_components, [m.aic(Xmoon) for m in models], label='AIC')plt.legend(loc='best')plt.xlabel('n_components');
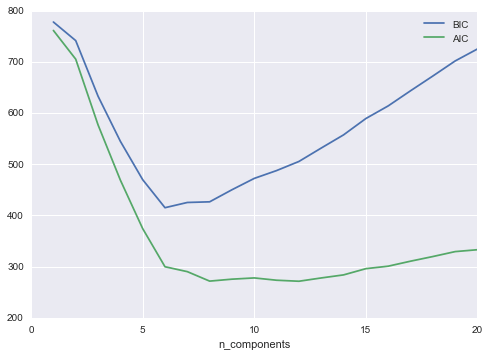
Số lượng cụm tối ưu là giá trị giảm thiểu AIC hoặc BIC, tùy thuộc vào xấp xỉ chúng ta muốn sử dụng. AIC cho chúng ta biết rằng lựa chọn của chúng ta với 16 thành phần trên có thể là quá nhiều: khoảng 8-12 thành phần sẽ là lựa chọn tốt hơn.Như thường là với kiểu vấn đề này, BIC đề xuất một mô hình đơn giản hơn.
Chú ý đến điểm quan trọng: lựa chọn số thành phần đo chỉ ra độ tốt của GMM như một bộ ước lượng mật độ, không phải độ tốt của GMM như một thuật toán phân cụm.
Ví dụ: GMM để tạo dữ liệu mới¶
Chúng ta vừa thấy một ví dụ đơn giản về việc sử dụng GMM như một mô hình sinh dữ liệu để tạo ra các mẫu mới từ phân phối được xác định bởi dữ liệu đầu vào.Ở đây chúng ta sẽ tiếp tục ý tưởng này và tạo ra những chữ số viết tay mới từ bộ văn bản chữ số tiêu chuẩn mà chúng ta đã sử dụng trước đó.
Để bắt đầu, hãy tải dữ liệu số sử dụng các công cụ dữ liệu của Scikit-Learn:
from sklearn.datasets import load_digitsdigits = load_digits()digits.data.shape
(1797, 64)
Tiếp theo chúng ta hãy vẽ đồ thị của 100 điểm đầu tiên để nhớ lại chính xác chúng ta đang nhìn vào cái gì:
def plot_digits(data): fig, ax = plt.subplots(10, 10, figsize=(8, 8), subplot_kw=dict(xticks=[], yticks=[])) fig.subplots_adjust(hspace=0.05, wspace=0.05) for i, axi in enumerate(ax.flat): im = axi.imshow(data[i].reshape(8, 8), cmap='binary') im.set_clim(0, 16)plot_digits(digits.data)

Chúng ta có gần 1.800 chữ số trong 64 chiều, và ta có thể xây dựng một GMM trên cơ sở này để tạo ra nhiều hơn.Các GMM có thể gặp khó khăn trong việc hội tụ trong không gian có số chiều cao như vậy, vì vậy ta sẽ bắt đầu bằng một thuật toán giảm chiều dữ liệu có thể đảo ngược.Ở đây, ta sẽ sử dụng một PCA đơn giản, yêu cầu nó giữ lại 99% phương sai trong dữ liệu đã được chiếu:
from sklearn.decomposition import PCApca = PCA(0.99, whiten=True)data = pca.fit_transform(digits.data)data.shape
(1797, 41)
Kết quả là 41 chiều, giảm gần 1/3 với ít mất thông tin.Dựa vào dữ liệu dự đoán này, chúng ta hãy sử dụng AIC để đánh giá số lượng thành phần GMM chúng ta nên sử dụng:
n_components = np.arange(50, 210, 10)models = [GMM(n, covariance_type='full', random_state=0) for n in n_components]aics = [model.fit(data).aic(data) for model in models]plt.plot(n_components, aics);
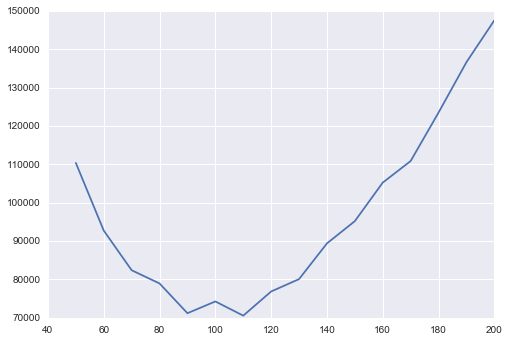
Có vẻ như khoảng 110 thành phần giảm thiểu AIC; chúng ta sẽ sử dụng mô hình này.Hãy nhanh chóng đưa nó vào dữ liệu và xác nhận rằng nó đã hội tụ:
gmm = GMM(110, covariance_type='full', random_state=0)gmm.fit(data)print(gmm.converged_)
True
Bây giờ chúng ta có thể vẽ mẫu của 100 điểm mới trong không gian 41 chiều này, sử dụng GMM như một mô hình sinh dữ liệu:
data_new = gmm.sample(100, random_state=0)data_new.shape
(100, 41)
Tiếp theo, chúng ta có thể sử dụng phép biến đổi nghịch đảo của đối tượng PCA để xây dựng các chữ số mới:
digits_new = pca.inverse_transform(data_new)plot_digits(digits_new)

Kết quả hầu hết trông giống như các chữ số có thể từ tập dữ liệu!
Hãy xem những gì chúng tôi đã làm ở đây: dựa trên một mẫu các chữ số được viết tay, chúng tôi đã mô hình hóa phân phối của dữ liệu đó một cách sao cho chúng tôi có thể tạo ra các mẫu hoàn toàn mới của các chữ số từ dữ liệu đó: đây là những “chữ số được viết tay” không xuất hiện cá nhân trong tập dữ liệu ban đầu, mà thay vào đó nắm bắt các đặc trưng chung của dữ liệu đầu vào như được mô hình hóa bởi mô hình hỗn hợp.Một mô hình sinh dữ liệu (generative model) của các chữ số như vậy có thể rất hữu ích như một thành phần của một bộ phân loại sinh dữ liệu Bayesian, như chúng ta sẽ thấy trong phần tiếp theo.









