Khái niệm KDE: Biểu đồ tần số
Như đã thảo luận trước đây, một trình ước lượng mật độ là một thuật toán mà nó cố gắng mô hình hóa phân phối xác suất mà đã tạo ra một tập dữ liệu.Đối với dữ liệu một chiều, bạn có thể đã quen thuộc với một trình ước lượng mật độ đơn giản: biểu đồ tần suất.Một biểu đồ tần suất chia dữ liệu thành các bin rời rạc, đếm số điểm rơi vào mỗi bin, và sau đó trực quan hóa kết quả một cách rõ ràng.
Ví dụ, hãy tạo ra một số dữ liệu được vẽ từ hai phân phối chuẩn:
def make_data(N, f=0.3, rseed=1): rand = np.random.RandomState(rseed) x = rand.randn(N) x[int(f * N):] += 5 return xx = make_data(1000)
Chúng ta đã từng thấy rằng biểu đồ histogram đếm chuẩn có thể được tạo ra bằng cách sử dụng chức năng plt.hist(). Bằng cách xác định tham số normed của histogram, chúng ta nhận được một histogram đã chuẩn hóa, trong đó chiều cao của các bin không phản ánh số lượng, mà thay vào đó phản ánh mật độ xác suất:
hist = plt.hist(x, bins=30, normed=True)
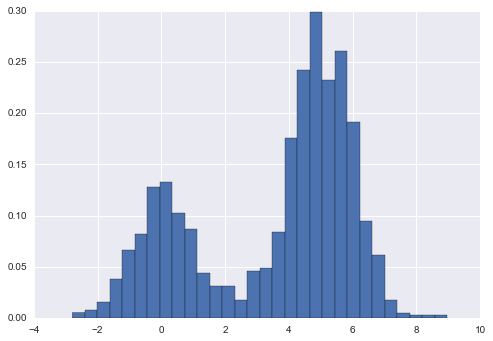
Lưu ý rằng đối với phân cấp bằng nhau, quy chuẩn hóa này chỉ thay đổi tỷ lệ trên trục y, giữ lại độ cao tương đối gần như giống như trong một biểu đồ tần số xây dựng từ đếm.Quy chuẩn hóa này được chọn sao cho tổng diện tích dưới biểu đồ là bằng 1, như chúng ta có thể xác nhận bằng cách nhìn vào đầu ra của hàm histogram:
density, bins, patches = histwidths = bins[1:] - bins[:-1](density * widths).sum()
1.0
Một trong những vấn đề khi sử dụng histogram như một bộ ước lượng mật độ là lựa chọn kích thước và vị trí của các bin có thể dẫn đến các biểu đồ có đặc điểm khác nhau về mặt chất lượng.Ví dụ, nếu chúng ta xem một phiên bản của dữ liệu này chỉ có 20 điểm, cách lựa chọn bin có thể dẫn đến một cách hiểu hoàn toàn khác về dữ liệu!Xem xét ví dụ sau đây:
x = make_data(20)bins = np.linspace(-5, 10, 10)
fig, ax = plt.subplots(1, 2, figsize=(12, 4), sharex=True, sharey=True, subplot_kw={'xlim':(-4, 9), 'ylim':(-0.02, 0.3)})fig.subplots_adjust(wspace=0.05)for i, offset in enumerate([0.0, 0.6]): ax[i].hist(x, bins=bins + offset, normed=True) ax[i].plot(x, np.full_like(x, -0.01), '|k', markeredgewidth=1)
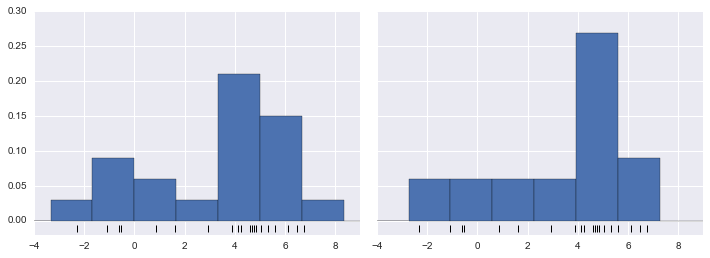
Bên trái, biểu đồ cột cho thấy đây là một phân phối hai đỉnh.Bên phải, chúng ta thấy một phân phối đơn điệu với đuôi dài.Mà không nhìn thấy mã trước đó, bạn có thể không đoán được rằng hai biểu đồ cột này được xây dựng từ cùng dữ liệu: với điều này trong tâm trí, làm thế nào bạn có thể tin tưởng vào trực giác của biểu đồ cột?Và chúng ta có thể cải thiện điều này như thế nào?
Với việc lùi lại, chúng ta có thể coi histogram như một tòa nhà được xếp chồng lên nhau, trong đó chúng ta xếp chồng một tòa nhà trong mỗi bin lên trên mỗi điểm trong dữ liệu.
fig, ax = plt.subplots()bins = np.arange(-3, 8)ax.plot(x, np.full_like(x, -0.1), '|k', markeredgewidth=1)for count, edge in zip(*np.histogram(x, bins)): for i in range(count): ax.add_patch(plt.Rectangle((edge, i), 1, 1, alpha=0.5))ax.set_xlim(-4, 8)ax.set_ylim(-0.2, 8)
(-0.2, 8)
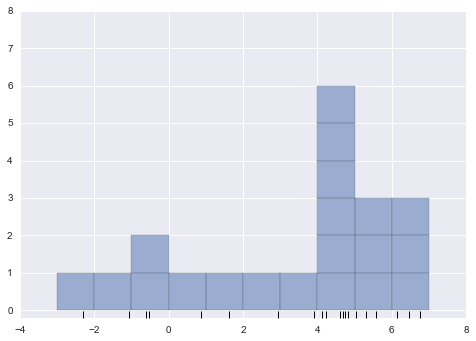
Vấn đề với hai cách phân bin của chúng ta bắt nguồn từ sự thật là chiều cao của ngăn xếp khối thường phản ánh không phải mật độ thực tế của điểm gần nhau, mà là do sự trùng hợp của cách các bin căn chỉnh với các điểm dữ liệu.Sự không căn chỉnh này giữa điểm và khối của chúng là nguyên nhân có thể gây ra kết quả kém của biểu đồ histogram ở đây.Nhưng nếu, thay vì xếp chồng các block căn chỉnh với các bin, chúng ta xếp chồng các block căn chỉnh với các điểm mà chúng đại diện?Nếu chúng ta làm điều này, các block sẽ không căn chỉnh, nhưng chúng ta có thể cộng dồn đóng góp của chúng tại mỗi vị trí trên trục x để tìm kết quả.Hãy thử điều này:
x_d = np.linspace(-4, 8, 2000)density = sum((abs(xi - x_d) < 0.5) for xi in x)plt.fill_between(x_d, density, alpha=0.5)plt.plot(x, np.full_like(x, -0.1), '|k', markeredgewidth=1)plt.axis([-4, 8, -0.2, 8]);
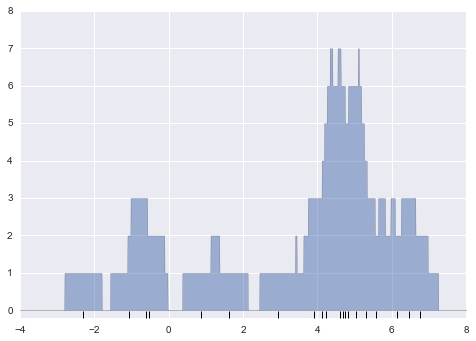
Kết quả trông hơi lộn xộn, nhưng đó là một phản ánh mạnh mẽ hơn về đặc điểm dữ liệu thực tế so với biểu đồ cổ điển.Tuy nhiên, những đường viền gồ ghề không hài lòng về mặt thẩm mỹ, cũng như không phản ánh bất kỳ thuộc tính thực sự nào của dữ liệu.Để làm mờ chúng, chúng ta có thể quyết định thay thế các khối tại mỗi vị trí bằng một hàm mờ, như hàm Gaussian.Hãy sử dụng một đường cong chuẩn hóa bình thường tại mỗi điểm thay vì một khối:
from scipy.stats import normx_d = np.linspace(-4, 8, 1000)density = sum(norm(xi).pdf(x_d) for xi in x)plt.fill_between(x_d, density, alpha=0.5)plt.plot(x, np.full_like(x, -0.1), '|k', markeredgewidth=1)plt.axis([-4, 8, -0.2, 5]);
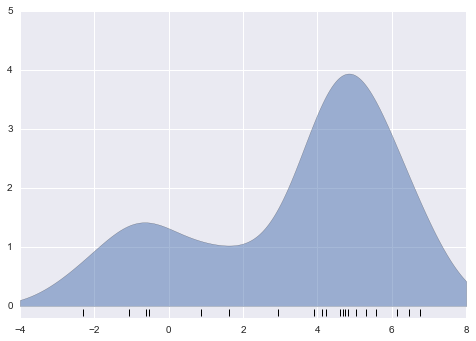
Đồ thị này đã được làm trơn, với một phân phối Gaussian đóng góp tại vị trí của mỗi điểm đầu vào, cung cấp một cái nhìn chính xác hơn về hình dạng của phân phối dữ liệu, và cũng có độ biến thiên ít hơn nhiều (tức là thay đổi ít hơn đáng kể khi có sự khác biệt trong quá trình lấy mẫu).
Những đồ thị cuối cùng này là các ví dụ về ước lượng mật độ kernel trong một chiều: ví dụ đầu tiên sử dụng một kernel được gọi là “tophat” và ví dụ thứ hai sử dụng một kernel Gaussian.Bây giờ chúng ta sẽ xem xét ước lượng mật độ kernel chi tiết hơn.
Ước lượng Mật độ Hạt nhân trong Thực tế¶
Các tham số tự do của ước lượng mật độ kernel là kernel, nghĩa là chỉ định hình dạng của phân phối được đặt tại mỗi điểm, và kernel bandwidth, nghĩa là điều khiển kích thước của kernel tại mỗi điểm.Trong thực tế, có nhiều kernel mà bạn có thể sử dụng cho ước lượng mật độ kernel: đặc biệt, thư viện Scikit-Learn KDE hỗ trợ sáu kernel, bạn có thể tìm hiểu thêm trong tài liệu Estimation Density của Scikit-Learn.
Dù có nhiều phiên bản của phân phối mật độ hạt nhân được cài đặt trong Python (đặc biệt là trong các gói SciPy và StatsModels), tôi thích sử dụng phiên bản của Scikit-Learn vì hiệu suất và linh hoạt của nó.Nó được cài đặt trong bộ ước lượng sklearn.neighbors.KernelDensity, xử lý phân phối mật độ hạt nhân trong nhiều chiều với một trong sáu nhân và một trong một vài chục phương pháp khoảng cách.Bởi vì phân phối mật độ hạt nhân có thể tốn nhiều công suất tính toán, bộ ước lượng của Scikit-Learn sử dụng một thuật toán dựa trên cây và có thể chọn thời gian tính toán để đạt được độ chính xác sử dụng các tham số atol (sai số tuyệt đối) và rtol (sai số tương đối).Dải thông số nhân, một tham số tự do, có thể được xác định bằng cách sử dụng các công cụ chuẩn hóa chéo của Scikit-Learn như chúng ta sẽ thấy trong thời gian sắp tới.
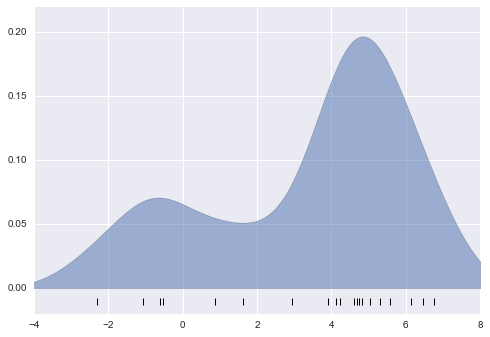
Hãy trước tiên cho thấy một ví dụ đơn giản về sao chép đồ thị trên bằng cách sử dụng bộ ước lượng KernelDensity trong Scikit-Learn:
from sklearn.neighbors import KernelDensity# instantiate and fit the KDE modelkde = KernelDensity(bandwidth=1.0, kernel='gaussian')kde.fit(x[:, None])# score_samples returns the log of the probability densitylogprob = kde.score_samples(x_d[:, None])plt.fill_between(x_d, np.exp(logprob), alpha=0.5)plt.plot(x, np.full_like(x, -0.01), '|k', markeredgewidth=1)plt.ylim(-0.02, 0.22)
(-0.02, 0.22)
Lựa chọn băng thông qua cross-validation¶
Lựa chọn băng thông trong KDE rất quan trọng để tìm ra một ước lượng mật độ phù hợp và là núm điều khiển điều chỉnh cân bằng giá trị gia – phương sai trong việc ước lượng mật độ: băng thông quá hẹp sẽ dẫn đến ước lượng có phương sai cao (tức là quá khớp), trong đó sự có mặt hoặc vắng mặt của một điểm duy nhất tạo ra một sự khác biệt lớn. Băng thông quá rộng sẽ dẫn đến một ước lượng có giá trị gia cao (tức là thiếu khớp) nơi cấu trúc trong dữ liệu bị mờ đi bởi hạt nhân rộng.
Có một lịch sử dài trong thống kê về các phương pháp để nhanh chóng ước tính băng thông tốt nhất dựa trên các giả định khá nghiêm ngặt về dữ liệu: nếu bạn tìm hiểu các triển khai KDE trong các gói SciPy và StatsModels, ví dụ như, bạn sẽ thấy các triển khai dựa trên một số quy tắc này.
Trong ngữ cảnh của học máy, chúng ta đã thấy rằng việc điều chỉnh siêu tham số như vậy thường được thực hiện thực nghiệm thông qua phương pháp chia tỉ lệ kiểm tra giao thức.Với ý này, bộ ước lượng KernelDensity trong Scikit-Learn được thiết kế sao cho nó có thể được sử dụng trực tiếp trong các công cụ tìm kiếm lưới tiêu chuẩn của Scikit-Learn.Ở đây chúng ta sẽ sử dụng GridSearchCV để tối ưu hóa băng thông cho tập dữ liệu trước đó.Bởi vì chúng ta đang xem xét một tập dữ liệu nhỏ như vậy, chúng tôi sẽ sử dụng chia tỉ lệ kiểm tra một người để tối thiểu hóa việc giảm kích thước bộ huấn luyện cho mỗi phép thử chia tỉ lệ kiểm tra:
from sklearn.grid_search import GridSearchCVfrom sklearn.cross_validation import LeaveOneOutbandwidths = 10 ** np.linspace(-1, 1, 100)grid = GridSearchCV(KernelDensity(kernel='gaussian'), {'bandwidth': bandwidths}, cv=LeaveOneOut(len(x)))grid.fit(x[:, None]);
Bây giờ chúng ta có thể tìm ra lựa chọn của băng thông mà tối đa hóa điểm số (mặc định là log-likelihood) :
grid.best_params_
{'bandwidth': 1.1233240329780276}
Băng thông tối ưu xảy ra rất gần với giá trị mà chúng ta đã sử dụng trong đồ thị ví dụ trước đó, trong đó băng thông là 1.0 (tức là chiều rộng mặc định của scipy.stats.norm).
Ví dụ: KDE trên một hình cầu¶
Có lẽ việc sử dụng KDE phổ biến nhất là trong việc biểu diễn đồ thị phân phối các điểm.Ví dụ, trong thư viện trực quan hóa Seaborn (xem Trực quan hóa với Seaborn), KDE được tích hợp sẵn và tự động sử dụng để trực quan hóa các điểm trong một hoặc hai chiều.
Ở đây chúng ta sẽ xem xét một cách sử dụng KDE phức tạp hơn để trực quan hóa phân phối.Chúng ta sẽ sử dụng một số dữ liệu địa lý có thể được tải với Scikit-Learn: phân bố địa lý của các quan sát được ghi lại về hai loài động vật Nam Mỹ, Bradypus variegatus (chú hà mã nâu cổ) và Microryzomys minutus (chuột gạo nhỏ rừng).
Với Scikit-Learn, chúng ta có thể lấy dữ liệu này như sau:
from sklearn.datasets import fetch_species_distributionsdata = fetch_species_distributions()# Get matrices/arrays of species IDs and locationslatlon = np.vstack([data.train['dd lat'], data.train['dd long']]).Tspecies = np.array([d.decode('ascii').startswith('micro') for d in data.train['species']], dtype='int')
Với dữ liệu này đã được tải, chúng ta có thể sử dụng công cụ Basemap (đã được đề cập trước đây trong Dữ liệu địa lý với Basemap) để vẽ đồ thị vị trí quan sát của hai loài trên bản đồ của Nam Mỹ.
from mpl_toolkits.basemap import Basemapfrom sklearn.datasets.species_distributions import construct_gridsxgrid, ygrid = construct_grids(data)# plot coastlines with basemapm = Basemap(projection='cyl', resolution='c', llcrnrlat=ygrid.min(), urcrnrlat=ygrid.max(), llcrnrlon=xgrid.min(), urcrnrlon=xgrid.max())m.drawmapboundary(fill_color='#DDEEFF')m.fillcontinents(color='#FFEEDD')m.drawcoastlines(color='gray', zorder=2)m.drawcountries(color='gray', zorder=2)# plot locationsm.scatter(latlon[:, 1], latlon[:, 0], zorder=3, c=species, cmap='rainbow', latlon=True);
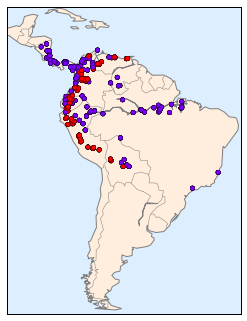
Rất tiếc, điều này không đưa ra một ý tưởng tốt về mật độ của loài này, vì các điểm trong phạm vi loài có thể chồng lấn lên nhau.Bạn có thể không nhận ra điều này khi nhìn vào biểu đồ này, nhưng có hơn 1.600 điểm được hiển thị ở đây!
Hãy sử dụng ước lượng mật độ lõi (kernel density estimation) để hiển thị phân phối này một cách dễ hiểu hơn: như một chỉ số mịn của mật độ trên bản đồ.Bởi vì hệ tọa độ ở đây nằm trên một bề mặt hình cầu thay vì một mặt phẳng phẳng, chúng ta sẽ sử dụng độ đo khoảng cách haversine, sẽ đại diện đúng các khoảng cách trên một bề mặt cong.
Ở đây có một chút mã boilerplate (một trong những nhược điểm của công cụ Basemap) nhưng ý nghĩa của mỗi khối mã nên rõ ràng:
# Set up the data grid for the contour plotX, Y = np.meshgrid(xgrid[::5], ygrid[::5][::-1])land_reference = data.coverages[6][::5, ::5]land_mask = (land_reference > -9999).ravel()xy = np.vstack([Y.ravel(), X.ravel()]).Txy = np.radians(xy[land_mask])# Create two side-by-side plotsfig, ax = plt.subplots(1, 2)fig.subplots_adjust(left=0.05, right=0.95, wspace=0.05)species_names = ['Bradypus Variegatus', 'Microryzomys Minutus']cmaps = ['Purples', 'Reds']for i, axi in enumerate(ax): axi.set_title(species_names[i]) # plot coastlines with basemap m = Basemap(projection='cyl', llcrnrlat=Y.min(), urcrnrlat=Y.max(), llcrnrlon=X.min(), urcrnrlon=X.max(), resolution='c', ax=axi) m.drawmapboundary(fill_color='#DDEEFF') m.drawcoastlines() m.drawcountries() # construct a spherical kernel density estimate of the distribution kde = KernelDensity(bandwidth=0.03, metric='haversine') kde.fit(np.radians(latlon[species == i])) # evaluate only on the land: -9999 indicates ocean Z = np.full(land_mask.shape[0], -9999.0) Z[land_mask] = np.exp(kde.score_samples(xy)) Z = Z.reshape(X.shape) # plot contours of the density levels = np.linspace(0, Z.max(), 25) axi.contourf(X, Y, Z, levels=levels, cmap=cmaps[i])
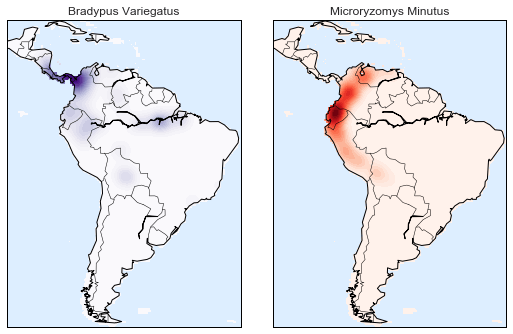
So sánh với biểu đồ phân tán đơn giản mà chúng ta ban đầu sử dụng, trực quan này tạo ra một hình ảnh rõ ràng hơn về phân bố địa lý của các quan sát về hai loài này.
Ví dụ: Không phải Naive Bayes¶
Ví dụ này tìm hiểu về phân loại sinh bayesian với KDE và minh họa cách sử dụng kiến trúc Scikit-Learn để tạo một bộ ước lượng tùy chỉnh.
Trong Suy Số Đại Học: Phân Loại Naive Bayes, chúng ta đã xem xét về phân loại Bayesian ngây thơ, trong đó chúng ta đã tạo ra một mô hình sinh học đơn giản cho mỗi lớp, và sử dụng những mô hình này để xây dựng một bộ phân loại nhanh chóng.Đối với Gaussian naive Bayes, mô hình sinh học là một phân phối Gaussian theo các trục đơn giản.Với một thuật toán ước tính mật độ như KDE, chúng ta có thể loại bỏ yếu tố “ngây thơ” và thực hiện cùng một phân loại với một mô hình sinh học phức tạp hơn cho mỗi lớp.Nó vẫn là phân loại Bayesian, nhưng không còn ngây thơ nữa.
Cách tiếp cận chung cho phân loại sinh ra là như sau:
Chia dữ liệu huấn luyện thành các nhãn.
Đối với mỗi tập hợp, thực hiện phù hợp với KDE để có được một mô hình sinh dữ liệu.Điều này cho phép bạn tính toán xác suất hợp lý $P(x~|~y)$ cho bất kỳ quan sát $x$ và nhãn $y$ nào.
Từ số lượng ví dụ cho mỗi lớp trong tập huấn luyện, tính toán xác suất trước của lớp, $P(y)$.
Đối với một điểm chưa biết $x$, xác suất hậu nghiệm cho mỗi lớp là $P(y~|~x) \propto P(x~|~y)P(y)$.Lớp mà làm tăng đỉnh của xác suất hậu nghiệm này được gán cho điểm đó.
Chia dữ liệu huấn luyện thành nhãn.
Đối với mỗi bộ dữ liệu, thực hiện việc khớp thông qua KDE để tạo ra một mô hình sinh dữ liệu.Điều này cho phép bạn tính toán xác suất hợp lý $P(x~|~y)$ cho bất kỳ quan sát $x$ và nhãn $y$ nào.
Từ số lượng các ví dụ của mỗi lớp trong tập huấn luyện, tính toán xác suất tiền lớp, $P(y)$.
Đối với một điểm không được biết là $x$, xác suất hậu nghiệm cho mỗi lớp là $P(y~|~x) \propto P(x~|~y)P(y)$.Lớp mà tối đa hóa xác suất hậu nghiệm này sẽ là nhãn được gán cho điểm đó.
Công thức tính toán đơn giản và dễ hiểu; phần khó khăn hơn là đặt vào khung Scikit-Learn để sử dụng cấu trúc tìm kiếm lưới và kiến trúc chia thành hai phần.
Đây là mã code thực hiện thuật toán trong framework Scikit-Learn; chúng ta sẽ đi qua nó theo khối mã:
from sklearn.base import BaseEstimator, ClassifierMixinclass KDEClassifier(BaseEstimator, ClassifierMixin): """Bayesian generative classification based on KDE Parameters ---------- bandwidth : float the kernel bandwidth within each class kernel : str the kernel name, passed to KernelDensity """ def __init__(self, bandwidth=1.0, kernel='gaussian'): self.bandwidth = bandwidth self.kernel = kernel def fit(self, X, y): self.classes_ = np.sort(np.unique(y)) training_sets = [X[y == yi] for yi in self.classes_] self.models_ = [KernelDensity(bandwidth=self.bandwidth, kernel=self.kernel).fit(Xi) for Xi in training_sets] self.logpriors_ = [np.log(Xi.shape[0] / X.shape[0]) for Xi in training_sets] return self def predict_proba(self, X): logprobs = np.array([model.score_samples(X) for model in self.models_]).T result = np.exp(logprobs + self.logpriors_) return result / result.sum(1, keepdims=True) def predict(self, X): return self.classes_[np.argmax(self.predict_proba(X), 1)]
Cấu trúc cơ bản của một bộ ước lượng tùy chỉnh¶
Xin mời ta đi qua mã này và thảo luận về các tính năng cần thiết:
from sklearn.base import BaseEstimator, ClassifierMixinclass KDEClassifier(BaseEstimator, ClassifierMixin): """Bayesian generative classification based on KDE Parameters ---------- bandwidth : float the kernel bandwidth within each class kernel : str the kernel name, passed to KernelDensity """
Mỗi trình ước lượng trong Scikit-Learn là một lớp, và việc này thuận tiện nhất cho lớp này để thừa kế từ lớp BaseEstimator cũng như mixin phù hợp, cung cấp chức năng tiêu chuẩn.
Ví dụ, ngoài những điều khác, ở đây BaseEstimator chứa các logic cần thiết để sao chép/mã hóa một trình ước lượng để sử dụng trong quá trình chéo xác thực, và ClassifierMixin xác định một phương thức score() mặc định được sử dụng bởi các lệnh như vậy.
Chúng tôi cũng cung cấp một chuỗi tài liệu, sẽ được IPython’s help chứa (xem Help và Tài liệu trong IPython).
Tiếp theo là phương thức khởi tạo lớp:
def __init__(self, bandwidth=1.0, kernel='gaussian'): self.bandwidth = bandwidth self.kernel = kernel
Đây là mã thực tế được thực thi khi đối tượng được khởi tạo với KDEClassifier().
Tiếp theo là phương thức fit(), trong đó chúng ta xử lý dữ liệu huấn luyện:
def fit(self, X, y): self.classes_ = np.sort(np.unique(y)) training_sets = [X[y == yi] for yi in self.classes_] self.models_ = [KernelDensity(bandwidth=self.bandwidth, kernel=self.kernel).fit(Xi) for Xi in training_sets] self.logpriors_ = [np.log(Xi.shape[0] / X.shape[0]) for Xi in training_sets] return self
Ở đây chúng ta tìm thấy các lớp duy nhất trong dữ liệu đào tạo, huấn luyện mô hình KernelDensity cho mỗi lớp và tính toán xác suất lớp dựa trên số lượng mẫu đầu vào.Cuối cùng, fit() luôn cần trả về self để chúng ta có thể nối các lệnh. Ví dụ:
label = model.fit(X, y).predict(X)
Lưu ý rằng mỗi kết quả của quá trình phù hợp được lưu thành kết quả với dấu gạch dưới ở cuối (ví dụ, self.logpriors_).Đây là quy ước được sử dụng trong Scikit-Learn để bạn có thể dễ dàng quét qua các thành viên của một estimator (sử dụng hoàn thiện bằng tab của IPython) và xem chính xác các thành viên nào được phù hợp với dữ liệu huấn luyện.
Mã HTML trên đề cập đến phần cuối cùng trong quá trình dự đoán nhãn trên dữ liệu mới:
def predict_proba(self, X): logprobs = np.vstack([model.score_samples(X) for model in self.models_]).T result = np.exp(logprobs + self.logpriors_) return result / result.sum(1, keepdims=True) def predict(self, X): return self.classes_[np.argmax(self.predict_proba(X), 1)]
Vì đây là một bộ phân loại xác suất, chúng tôi trước tiên triển khai predict_proba() mà trả về một mảng xác suất lớp có hình dạng [n_samples, n_classes].
Cuối cùng, phương thức predict() sử dụng những xác suất này và đơn giản trả về lớp có xác suất lớn nhất.
Sử dụng bộ định hình tùy chỉnh của chúng tôi¶
Hãy thử bộ ước lượng tùy chỉnh này trên một vấn đề chúng ta đã từng thấy trước đây: phân loại số viết tay.Ở đây chúng ta sẽ tải các chữ số và tính điểm xác thực chéo cho một loạt các băng thông ứng viên bằng cách sử dụng meta-estimator GridSearchCV (hãy xem lại Hyperparameters and Model Validatation):
from sklearn.datasets import load_digitsfrom sklearn.grid_search import GridSearchCVdigits = load_digits()bandwidths = 10 ** np.linspace(0, 2, 100)grid = GridSearchCV(KDEClassifier(), {'bandwidth': bandwidths})grid.fit(digits.data, digits.target)scores = [val.mean_validation_score for val in grid.grid_scores_]
Tiếp theo, chúng ta có thể vẽ đồ thị điểm số xác thực giao động theo hàm bandwidth:
plt.semilogx(bandwidths, scores)plt.xlabel('bandwidth')plt.ylabel('accuracy')plt.title('KDE Model Performance')print(grid.best_params_)print('accuracy =', grid.best_score_)
{'bandwidth': 7.0548023107186433}accuracy = 0.966611018364
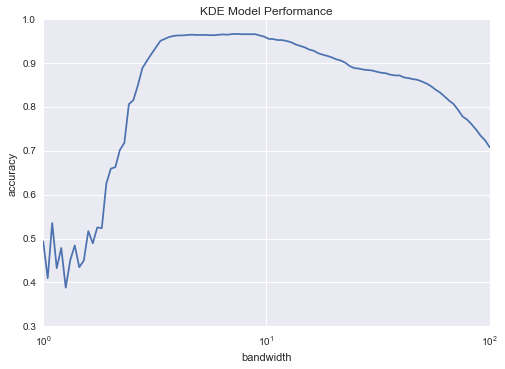
Ta thấy rằng bộ phân loại Bayesian không ngây thơ này đạt được độ chính xác xác thực qua kiểm tra chéo lên tới hơn 96%; điều này so sánh với khoảng 80% cho phân loại Bayesian ngây thơ:
from sklearn.naive_bayes import GaussianNBfrom sklearn.cross_validation import cross_val_scorecross_val_score(GaussianNB(), digits.data, digits.target).mean()
0.81860038035501381
Một lợi ích của một bộ phân loại tự sinh như vậy là sự minh bạch trong kết quả: đối với mỗi mẫu không biết, chúng ta không chỉ nhận được một phân loại xác suất, mà còn là một mô hình đầy đủ về phân phối các điểm chúng ta đang so sánh nó với!Nếu muốn, điều này mang lại một cửa sổ trực quan vào các lý do cho một phân loại cụ thể mà các thuật toán như SVM và random forests thường làm mờ.
Nếu bạn muốn tiến xa hơn, có thể thực hiện một số cải tiến cho mô hình phân loại KDE của chúng tôi:
- Chúng ta có thể cho phép băng thông trong mỗi lớp biến đổi độc lập
- Chúng ta có thể tối ưu các băng thông này không dựa trên điểm dự đoán của chúng, mà dựa trên khả năng của dữ liệu huấn luyện dưới mô hình sinh trong mỗi lớp (tức là sử dụng các điểm số từ
KernelDensitychính nó thay vì độ chính xác dự đoán toàn cục)
Kết thúc cùng, nếu bạn muốn rèn luyện việc xây dựng một bộ phân loại riêng của mình, bạn có thể thử xây dựng một bộ phân loại Bayesian tương tự sử dụng Mô hình Hỗn hợp Gaussian thay vì KDE.







