Feature matching là một kỹ thuật quan trọng trong xử lý ảnh, được sử dụng để tìm kiếm các điểm tương ứng giữa hai hình ảnh của cùng một bối cảnh hoặc đối tượng. Feature matching đóng vai trò quan trọng trong các ứng dụng như Object detection and Tracking, chụp ảnh Panorama, Tái tạo hình ảnh 3D và thực tế ảo AR. Hiện nay các phương pháp feature matching được chia thành hai nhóm chính: phương pháp truyền thống và phương pháp dựa trên deep learning, trong đó, các phương pháp dựa trên deep learning đã phát triển mạnh mẽ trong những năm gần đây nhờ vào nhu cầu xây dựng các ứng dụng AI liên quan.
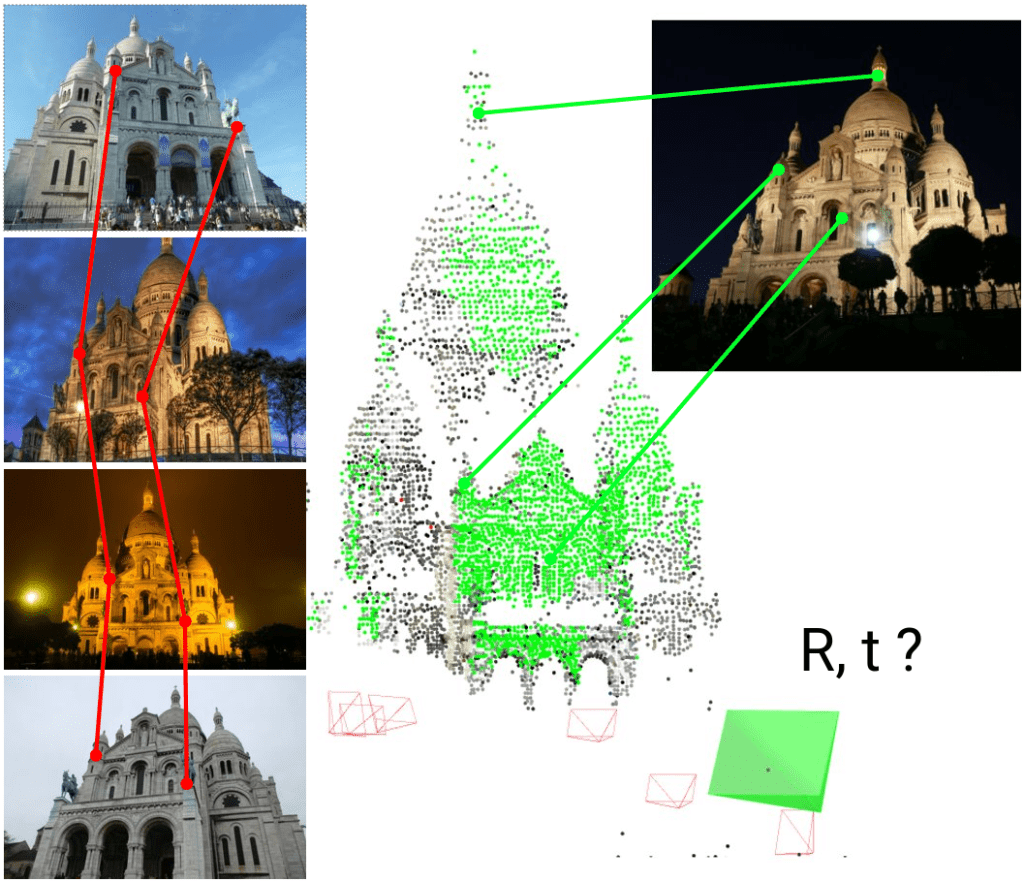
Ý tưởng cơ bản của Feature Matching trong xử lý ảnh
Mặc dù có nhiều phương pháp Feature matching khác nhau, những phương pháp này thường cố gắng thực hiện những bước như sau:
Trích xuất các điểm đặc trưng (Keypoint extraction): Đầu tiên ta cần xác định các điểm đặc trưng (keypoints) trong hình ảnh. Keypoints thường là những vị trí nổi bật như góc, cạnh, hoặc vùng có sự thay đổi rõ rệt về cường độ sáng (intensity). Hầu hết các phương pháp Feature matching truyền thống đều áp dụng phương pháp này.
Mô tả đặc trưng (Feature Description): Khi trích xuất các keypoints, ta đồng thời cũng trích xuất các đặc điểm trên hình của keypoint đó, các đặc điểm này thường được mô tả bằng một vector, gọi là descriptor. Vector này giúp phân biệt một keypoint với các keypoint khác, descriptor thường chứa thông tin về đặc tính cục bộ của vùng xung quanh nó, ví dụ như các thay đổi về góc nhìn, tỷ lệ, hoặc ánh sáng.
So khớp đặc trưng (Feature Matching): So sánh các vector mô tả giưa hai hình ảnh để tìm ra các cặp điểm tương ứng bằng 1 số phương pháp thường dùng như khoảng cách Euclidean, khoảng cách Hamming, sau đó chọn cặp có khoảng cách nhỏ nhất (nearest neighbor). Để tăng độ chính xác và giảm số lượng tính toán, ta thường áp dụng thêm 1 số kỹ thuật lọc (ví dụ như ratio test của Lowe: chỉ chấp nhận cặp khớp nếu khoảng cách nhỏ nhất nhỏ hơn một ngưỡng so với khoảng cách thứ hai nhỏ nhất)

Các Phương Pháp Feature Decscription Phổ Biến
SIFT (Scale-Invariant Feature Transform)

Như ta đã biết, Keypoints thường là những vị trí nổi bật như góc, cạnh, hoặc vùng có sự thay đổi rõ rệt về cường độ sáng (intensity). Ta có rất nhiều thuật toán cho phép tìm ra các góc cạnh trên ảnh (tham khảo thuật toán Harris Corner Detector là một ví dụ).
Nhưng có một vấn đề, một vài góc/cạnh, khi phóng to lên sẽ không còn đặc trưng đó nữa (nó trở nên trơn hơn – ảnh bên dưới). Và SIFT đã ra đời để giải quyết vấn đề đó.
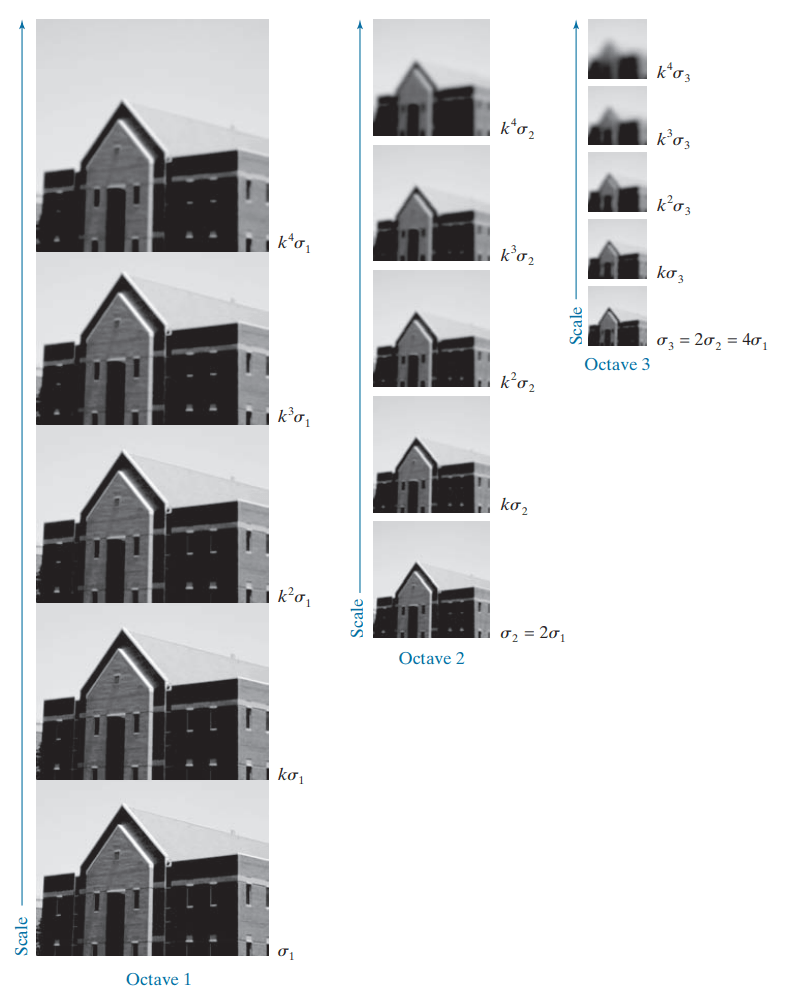
Đầu tiên, ta tạo ra nhiều phiên bản với các kích thước tỉ lệ khác nhau của ảnh gốc, ứng với mỗi tỉ lệ, ta cũng áp dụng các Gaussian filter với các kích thước khác nhau để tạo ra nhiều phiên bản như hình bên dưới.
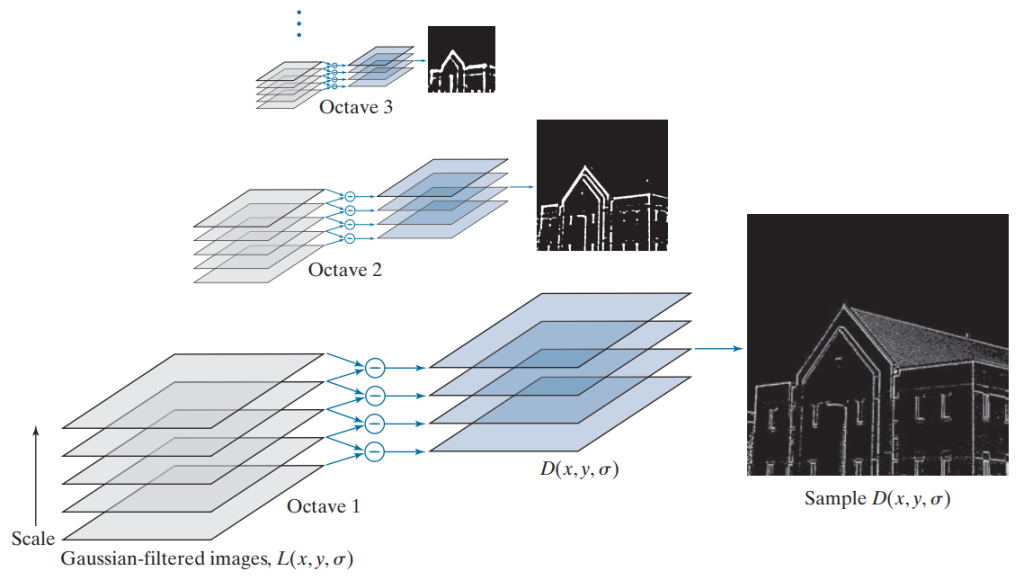
Difference of Gaussians (DoG) – tạo ra bằng cách lấy hiệu của hai ảnh mờ liên tiếp – kết quả là ta thu được nhiều layer DoG tương ứng với các tỉ lệ ảnh. Bằng việc so sánh mỗi điểm trên từng layer với các layer tương ứng với các tỉ lệ ảnh liền kề, ta có thể tìm được những điểm đặc trưng (keypoints) tiềm năng, là những điểm có giá trị cực đại hoặc cực tiểu trong không gian tỷ lệ.
Không gian tỉ lệ của một điểm ảnh trên 1 layer bất kì chính là:
- 8 điểm xung quanh điểm đó trong cùng 1 layer
- 9 điểm xung quanh điểm đó trong layer với tỉ lệ lớn hơn liền kề
- 9 điểm xung quanh điểm đó trong layer với tỉ lệ nhỏ hơn liền kề
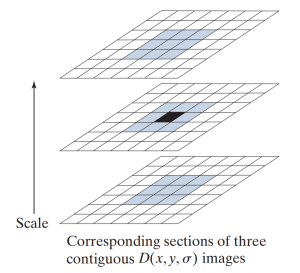
Vấn đề là, phương pháp này tốn nhiều chi phí tính toán và đồng thời cũng tạo ra rất nhiều keypoint thừa (tạo ta do nhiễu hoặc thay đổi cường độ sáng). Vì vậy, một số bước lọc, ví dụ như loại bỏ các keypoint có cường độ sáng (brightness) thấp hoặc độ tương phản (contrast) thấp.

Cuối cùng, các keypoint được xác định đặc trưng thông qua việc tính sự thay đổi về màu sắc (gradient) của khu vực 16×16 xung quanh keypoint đó. Phương pháp này sẽ tạo ra một ma trận 4×4 mà mỗi ô của ma trận biểu diễn cường độ gradient của 8 hướng, và ta có thể xây dựng 1 vector 128 chiều tương ứng, gọi là Descriptor.
Thực ra giải thích cho người đọc hiểu toàn bộ thuật toán SIFT ở đây không phải là việc dễ dàng, vì vậy, hãy xem lời giải thích trên như một gợi ý và có thể tìm đọc chi tiết hơn về SIFT ở các bài blog khác.
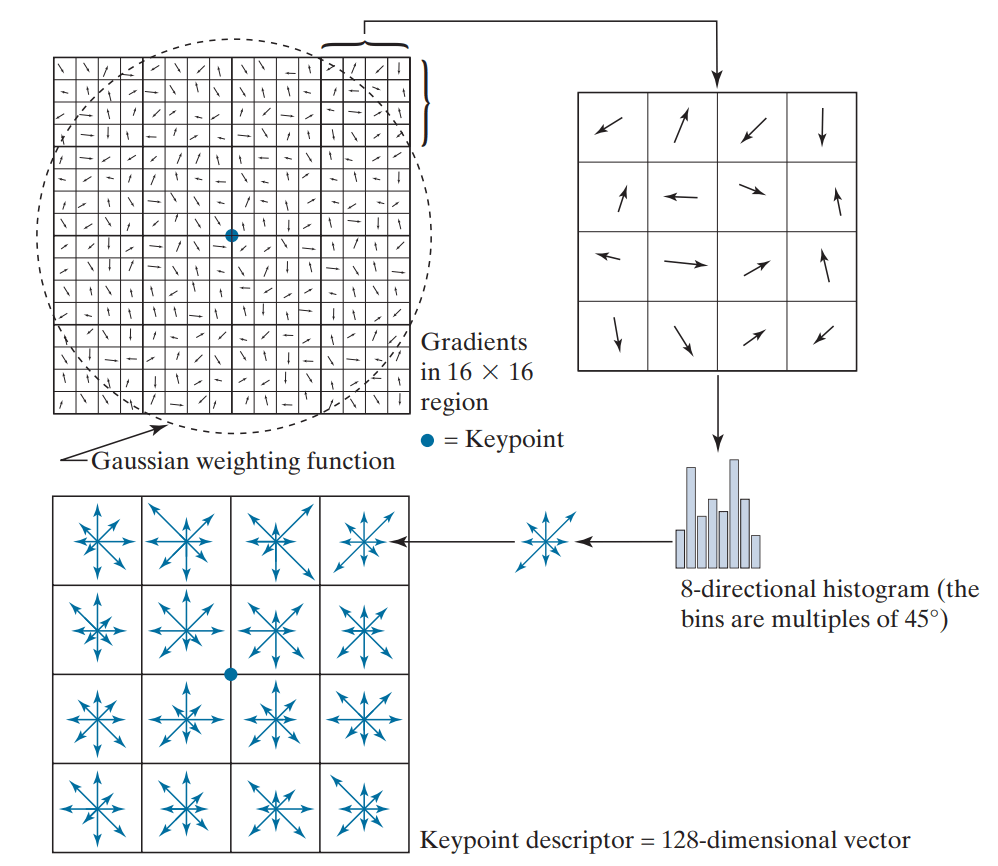
Còn lại là về việc Feature Matching giữa 2 ảnh, điều này có thể thực hiện rất dễ dàng bằng cách tìm ra các điểm Keypoint giống nhau nhất giữa 2 bức ảnh thông qua việc Brute Force tìm khoảng cách bé nhất giữa tất cả các Vector Decriptor tương ứng với các keypoints. Những metric được dùng thường là khoảng cách Euclide.

SURF (Speeded-Up Robust Features)
SURF là một phiên bản cải tiến nhanh hơn của SIFT, vẫn đảm bảo được những khả năng matching những feature xoay và tỉ lệ như SIFT, nhưng với tốc độ nhanh hơn thông qua 1 số thay đổi:
- Phát hiện điểm đặc trưng: Thay vì dùng Gaussian filter như SIFT, SURF sử dụng box filter (Lấy avaverage của kernel thay vì dùng làm Gaussian), mang lại rất nhiều hiệu quả về mặt tính toán. Dựa trên ma trận Hessian (Ma trận hessian thường dùng để tìm ra độ cong của một hàm, 1 ứng dụng của ma trận Hessian là để tìm độ cong của hàm loss trong deep learning) để phát hiện các điểm đặc trưng.
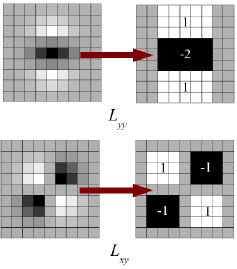
- Không gian tỉ lệ: SURF không giảm kích thước ảnh mà tăng kích thước của bộ lọc để mô phỏng các mức tỉ lệ khác nhau, bởi vì thay đổi kích thước kernel thì nhanh hơn so với resize ảnh.
- Xác định hướng: Thay vì sử dụng Gradient như trong SIFT, SURF sử dụng bộ lọc Haar wavelet (Vertical và Horizontal) trong 1 bán kính 6s (s là hệ số) lân cận để gán hướng cho điểm đặc trưng. Các giá trị cũng được nhân với trọng số (weighted) bằng một hàm Gaussian có tâm là điểm đặc trưng (Hàm Gaussian giúp giảm ảnh hưởng của các pixel xa điểm đặc trưng, và ưu tiên những thông tin ở gần điểm đặc trưng).
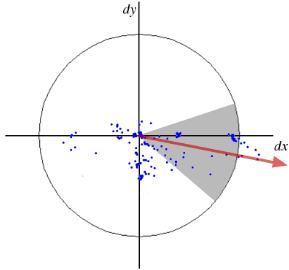
Mô tả đặc trưng: Tạo vector mô tả (thường 64 chiều, ngắn hơn SIFT) dựa trên tổng các phản hồi Haar wavelet theo các hướng khác nhau. Cụ thể là một vùng 20s*20s (s là hệ số) được lấy quanh điểm đặc trưng và chia thành 4×4=16 vùng, với mỗi vùng ta xây dựng được một vector v = (∑dx, ∑dy, ∑|dx|, ∑|dy|) (lần lượt là Tổng phản hồi ngang, tổng phản hồi dọc, tổng giá trị tuyệt đối ngang, tổng giá trị tuyệt đối dọc). Từ đó, ta có một vector 4*4*4=64 chiều.
Về cơ bản ta có thể thấy SURF là một phiên bản nâng cấp của SIFT, trong đó, các bước xử lý của SIFT đều được thay bằng các phương pháp cải thiện tốc độ hơn, qua đó tăng tốc độ xử lý lên rất nhiều mà không cần đánh đổi về độ chính xác. SURF hoạt động tốt cả trên các ảnh bị mờ và xoay, nhưng sẽ hoạt động kém hơn khi có sự hay đổi về góc nhìn của bức ảnh hoặc các biến đổi trên ảnh.
ORB (Oriented FAST and Rotated BRIEF)
ORB là một thuật toán kết hợp giữa FAST (Features from Accelerated Segment Test) để phát hiện điểm đặc trưng và BRIEF (Binary Robust Independent Elementary Features) để mô tả đặc trưng. Thuật toán này được sử dụng phổ biến hơn gần đây so với SURF và SIFT vì nó nhanh, nhẹ và không bị ràng buộc bởi bản quyền như SIFT hay SURF.
- Phát hiện điểm đặc trưng: FAST (Features from Accelerated Segment Test) kiểm tra một tập hợp các pixel xung quanh một pixel trung tâm (một vòng tròn 16 pixel). Nếu có đủ số pixel trong vòng này có giá trị cường độ sáng khác biệt đáng kể (sáng hơn hoặc tối hơn) so với pixel trung tâm, thì pixel đó được coi là một điểm đặc trưng. Phương pháp này bỏ qua nhiều đặc điểm trong ảnh so với DoG của SIFT hay ma trận Hessian của SURF, vì vậy nó cũng tỏ ra kém hiệu quả hơn và không nhạy cảm với tỉ lệ và hướng. Tuy nhiên nó cực kì nhanh, vì vậy được sử dụng nhiều cho các trường hợp ứng dụng cần realtime.
- Mô tả điểm đặc trưng: BRIEF (Binary Robust Independent Elementary Features) tạo ra một binary descriptor bằng cách so sánh cường độ sáng của các cặp pixel được chọn ngẫu nhiên trong vùng lân cận của điểm đặc trưng. Kết quả là một chuỗi bit (0 hoặc 1) biểu thị mối quan hệ sáng/tối giữa các cặp pixel. Bạn sẽ tự hỏi, mới mỗi điểm đặc trưng 16*16 thì sẽ có rất nhiều cách chọn các điểm để so sánh, vậy ra sẽ chọn điểm nào. Câu trả lời là “ngẫu nhiên”, và ngẫu nhiên như thế nào thị bạn có thể tham khảo hình bên dưới.
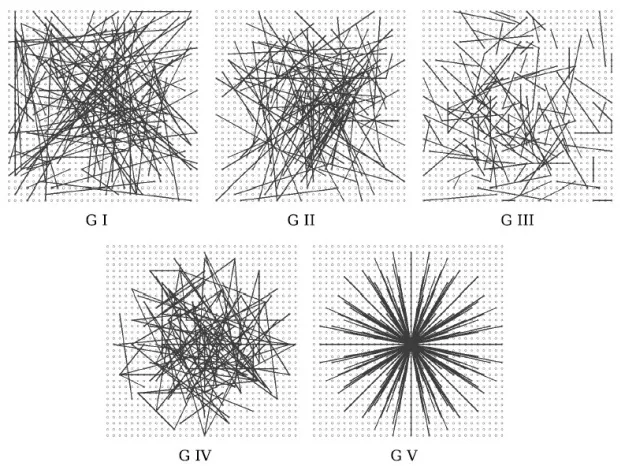
- Uniform(G I): Các cặp được lựa chọn ngẫy nhiên theo phân phối chuẩn
- Gaussian(G II): Các cặp điểm được lựa chọn ngẫu nhiên theo phân phối Gaussian với độ lệch chuẩn là bán kính 0.04 * S² xung quanh điểm đặc trưng.
- Gaussian(G III): điểm đầu tiên được lựa chọn ngẫu nhiên theo phân phối Gaussian với bán kính 0.04 * S² xung quanh điểm đặc trưng. Điểm thứ 2 được lựa chọn ngẫu nhiên theo phân phối Gaussian với bán kính 0.01 * S² xung quanh điểm đầu tiên.
- Coarse Polar Grid(G IV): tọa độ của cặp điểm được lựa chọn ngẫu nhiên trong vòng tròn xung quanh điểm đặc trưng.
- Coarse Polar Grid(G V): Điểm đầu tiên ứng với điểm đặc trưng (0, 0) và điểm thứ 2 được lựa chọn ngẫu nhiên trong vòng tròn xung quanh điểm đặc trưng.
Cả FAST và BRIEF đều sửa dụng các phương pháp để tối thiểu nhu cầu tính toán nhất có thể, ví dụ như phép so sánh và đếm như trong FAST thay vì tính toán ma trận, sử dụng binary descriptor hay vì dùng một vector thực để mô tả điểm đặc trưng, do đó ORB có tốc độ cực kỳ nhanh và được sử dụng nhiều trong các ứng dụng realtime.
Các phương pháp Feature Matching
Sau khi đã tìm ra các điểm đặc trưng của một bức ảnh, mục tiêu của ta là làm sao so khớp được những mnội dung giống nhau giữa 2 bức ảnh khác nhau. Ta có thể thực hiện việc này bằng các tìm kiếm các điểm đặc trưng giống nhau giữa 2 bức ảnh theo một trong các phương pháp bên dưới:
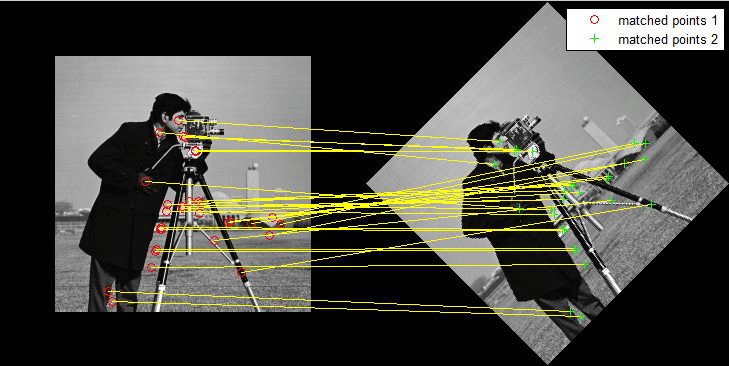
- Brute-Force Matching: Với mỗi điểm đặc trưng trên ảnh thứ nhất, ta so sánh nó với mọi điểm đặc trưng trên ảnh thứ 2 để tìm ra điểm đặc trưng giống nhất, khi đó, 2 điểm này được xem là khớp với nhau. Ta thường sử dựng khoảng các Euclide giữa 2 vector trưng như là một phương pháp để so sánh độ khác nhau giữa 2 điểm đặc trưng.
- K-Nearest Neighbors – KNN Matching: tương tự như Brute-formatching, ta tìm “k” điểm đặc trưng gần nhất trên ảnh thứ 2 cho mỗi điểm đặc trưng trên ảnh thứ nhất dựa trên thước đo khoảng cách. Phương pháp này cho phép ta có nhiều lựa chọn hơn để xem xét điểm nào trên là điểm đặc trưng tương ứng.
Mặc dù 2 phương pháp trên dễ dàng áp dụng, chúng đòi hỏi nhiều tính toán khi số lượng các điểm đặc trưng tăng lên (Khi bức ảnh có nhiều đặc điểm hoặc khi kích thước ảnh lớn hơn, nhiều chi tiết hơn). Khi đó, một phương pháp thường được người ta sử dụng hơn đó là RANSAC (Bấm để xem bài viết chi tiết hơn về thuật toán RANSAC)
RANSAC (Random Sample Consensus): là một phương pháp lặp dùng để ước lượng tham số của một mô hình toán học từ tập dữ liệu có chứa ngoại lệ (outliers). Trong feature matching, RANSAC được sử dụng để tìm tập hợp các cặp khớp bền vững bằng cách lặp lại việc chọn ngẫu nhiên các tập con và tìm ra những cặp điểm khớp. Phép biến đổi có số lượng điểm nội tại (inliers) (có thể hiểu là số lượng cặp điểm khớp) cao nhất sẽ được chọn.
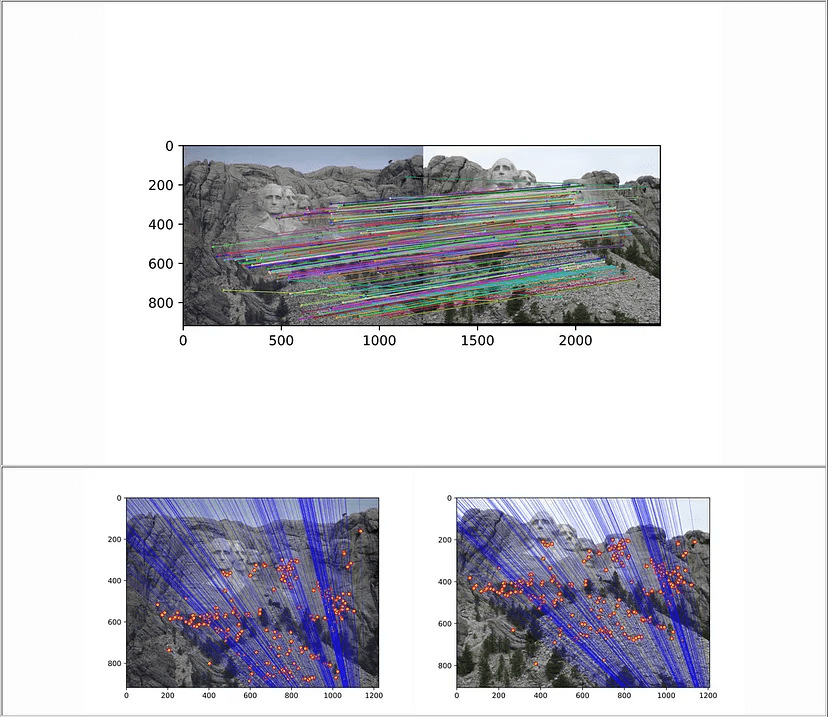
Ở trên là những mô tả cơ bản theo cách mình hiểu về các thuật toán so khớp ảnh (Feature Matching) trong xử lý ảnh, những thuật toán này thường được dùng rất nhiều trong các ứng dụng hiện đại như nhận diện vật thể, theo dõi chuyển động, tạo ảnh panorama, chống rung video, tái tạo mô hình 3D từ ảnh 2D,…..
Nếu bài biết này có ích cho bạn hoặc có điều gì sai sót cần mình sửa chữa lại, đừng ngại để lại comment nhé.








