1. Giới thiệu về RANSAC
Random sample consensus (RANSAC) là một phương pháp lặp dùng để xây dựng xấp xỉ một mô hình toán học từ một tập hợp dữ liệu các điểm dữ liệu có chứa các giá trị ngoại lệ (vd Linear Regression cũng là một phương pháp xây dựng mô hình toán học cho một tập hợp điểm), sao cho giá trị ngoại lệ không ảnh hưởng đến mô hình. Theo một cách hiểu khác, RANSAC cũng được coi là một phương pháp xác định các điểm ngoại lai (outliers). Nó là một thuật toán không xác định (non-deterministic) theo nghĩa là nó tạo ra một kết quả tốt với một xác suất nhất định, nói ngắn gọn, kết quả của RANSAC sẽ tin cậy hơn khi bạn thực hiện nhiều vòng lặp hơn, và việc này có thể kéo dài đến vô hạn.
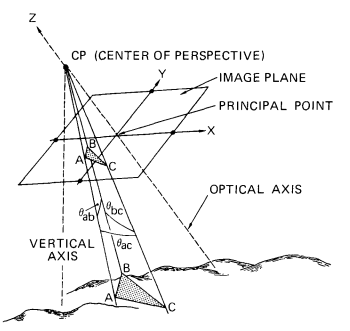
Thuật toán được Fischler và Bolles công bố lần đầu tiên tại SRI International vào năm 1981. Họ sử dụng RANSAC để giải Bài toán Xác định Vị trí (Location Determination Problem – LDP), trong đó mục tiêu là xác định các điểm trong không gian chiếu lên một hình ảnh thành một tập hợp các điểm mốc với các địa điểm đã biết.
2. Chi tiết thuật toán RANSAC
RANSAC sử dụng phương pháp chọn tập con ngẫu nhiên lặp lại. Giả sử dữ liệu của chúng ta bao gồm các điểm dữ liệu trong không gian (bao gồm các điểm trong và điểm ngoại lai – outliers chưa được xác định) và tập hợp xác điểm trong có thể xấp xỉ thành một mô hình toán học (vd trong trường hợp này là 1 đường thẳng trong không gian 2 chiều), và những điểm ngoại lai là những điểm không phù hợp với mô hình này. RANSAC giả định rằng luôn có 1 tập hợp nhỏ các điểm trong, sao cho tồn tại một mô hình toán học thỏa mãn được tập hợp điểm dữ liệu đó với 1 sai số cho phép.


Về cơ bản, RANSAC sử dụng một phương pháp bỏ phiếu: Các điểm dữ liệu trong tập dữ liệu sẽ bỏ phiếu cho một hay nhiều mô hình, Việc bỏ phiếu dựa trên hai giả định: rằng các điểm nhiễu sẽ không liên tục bỏ phiếu cho một (hoặc vài) mô hình nhất định nào.
Thuật toán RANSAC về cơ bản bao gồm hai bước được lặp đi lặp lại:
- Trong bước đầu tiên, một con các điểm dữ liệu được chọn ngẫu nhiên từ tập dữ liệu đầu vào. Một mô hình sẽ được xây dựng bằng cách xấp xỉ các điểm dữ liệu trên tập hợp này (giả sử tập dữ liệu này đủ nhiều để có thể xây dựng nên một mô hình)
- Trong bước thứ hai, thuật toán kiểm tra điểm dữ liệu nào phù hợp với mô hình ở bước đầu tiên. Một phần tử dữ liệu sẽ được coi là ngoại lệ nếu nó không phù hợp với mô hình trong một ngưỡng lỗi nhất định.
Tập hợp các điểm trong phù hợp với mô hình được gọi là tập hợp đồng thuận (consensus). Thuật toán RANSAC sẽ lặp đi lặp lại hai bước trên cho đến khi tập hợp đồng thuận đủ nhiều trong trong số lượng vòng lặp nhất định.
Đầu vào của thuật toán RANSAC là một tập hợp các điểm dữ liệu, một cách để điều chỉnh một số loại mô hình với các quan sát và một số tham số tin cậy. RANSAC đạt được mục tiêu của mình bằng cách lặp lại các bước sau:
- Chọn một tập hợp con ngẫu nhiên của dữ liệu gốc. Gọi tập hợp con này là tập hợp con giả định.
- Một mô hình được xây dựng từ tập hợp giả định.
- Mô hình này sẽ kiểm tra tất cả các điểm dữ liệu khác. Những điểm phù hợp tốt với mô hình với một sai số nhất định, được coi là một phần của tập hợp đồng thuận.
- Một mô hình là tốt nếu có đủ nhiều điểm được xếp vào tập hợp đồng thuận.
- Sau đó, mô hình có thể được cải thiện bằng cách sử dụng tất cả các điểm dữ liệu trong tập hợp đồng thuận.
Quy trình này được lặp đi lặp lại một số lần nhất định, mỗi lần tạo ra một mô hình, mô hình này sẽ có 2 trường hợp: bị từ chối vì có quá ít điểm đồng thuận hoặc có nhiều điểm đồng thuận hơn so với các mô hình trước đó. Trong trường hợp sau, chúng ta lưu mô hình lại.
Ưu điểm và nhược điểm
Một ưu điểm của RANSAC là khả năng ước lượng. Tức là RANSAC có thể tạo ra các mô hình có mức độ chính xác cao ngay cả khi có một số lượng đáng kể các giá trị ngoại lai trong tập dữ liệu. Một nhược điểm của RANSAC là nó không có giới hạn trên về thời gian cần thiết để tính toán (trừ khi chúng ta vét cạn mọi tập con). Khi số lần lặp bị giới hạn, mô hình thu được có thể không tối ưu và thậm chí có thể hoàn toàn không phù hợp. Theo đó, RANSAC đưa ra một sự đánh đổi: tính toán số lần lặp lại nhiều hơn và xác suất tạo ra một mô hình hợp lý sẽ tăng lên và ngược lại.
Vậy chúng ta cần bao nhiêu vòng lặp là đủ?
Để đạt được xác suất thành công là p thì chúng ta sẽ cần số vòng lặp là:
Hơn nữa, RANSAC không phải lúc nào cũng có thể tìm được bộ tối ưu ngay cả đối với các bộ bị ô nhiễm vừa phải và nó thường hoạt động kém khi số lượng các điểm trong (inliers) ít hơn 50%.
Mô hình Optimal RANSAC có khả năng khắc phuc vấn đề này và tìm ra mô hình tối ưu ngay cả khi nhiễu> 95%.
Một nhược điểm khác của RANSAC là nó yêu cầu thiết lập các ngưỡng cho hàm mất mát.
3. Bắt tay vào làm thử xem sao
Đầu tiên ta import 1 số thư viện để làm demo
import random
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegressionTa tạo ngẫu nhiên 1 mảng gồm 100 phần tử sao cho chúng tạo thành tập hợp các điểm trong, rải rác xung quanh đường thẳng y=ax+b, ở đây, mình tạo các điểm với sai số không quá 10 so với đường thẳng cơ sở
a = 1
b = np.random.uniform(low=-10, high=10, size=(100,))
x_points = np.random.uniform(low=0, high=100, size=(100,))
y_points = a * x_points + b
d1 = np.stack([x_points,y_points],axis=1)
plt.scatter(d1[:,0],d1[:,1])
plt.show()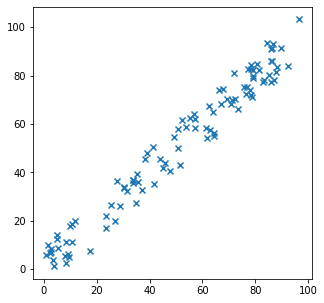
Kế đó tạo thêm 100 điểm khác rải rác bên ngoài tượng trưng cho outliers, sau đó gộp cả 2 mảng lại để được tập hợp data mẫu
d2 = np.random.uniform(low=0, high=100, size=(100,2))
plt.figure(figsize=(5, 5))
plt.scatter(d2[:,0],d2[:,1],marker = 'x')
plt.show()data = np.concatenate((d1, d2), axis=0)
plt.figure(figsize=(5, 5))
plt.scatter(data[:,0],data[:,1],marker = 'x')
plt.show()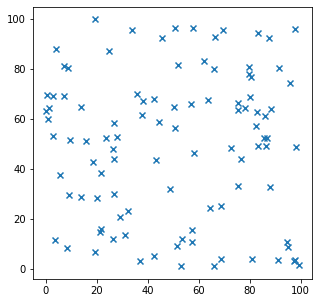
OK, giờ data đã sẵn sàng, ta sẽ áp dụng RANSAC vào bài toán này để tìm ra mô hình tối ưu cho dữ liệu này. Trước hết, ta cần xác định một số tham số và ngưỡng trước khi đi vào thuật toán.
Đầu tiên, Kích thước tập con là bao nhiêu? kích thước tập con phải đủ nhỏ để tiết kiệm chi phí tính toán, và đủ lớn để hình thành 1 mô hình có thể tin cậy, ở đây mình chọn s = 10
Tiếp theo là ngưỡng sai số trong khi bỏ phiếu, mình sẽ chấp nhận những điểm với sai số không quá 15 so với mô hình
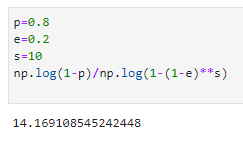
Cuối cùng là số vòng lặp, theo công thức ở trên, mình ước tính tỉ lệ nhiễu là khoảng 20%, kích thước tập con là s=10, và xác xuất mình kì vọng là 80% để đạt được mô hình mong muốn, vì vậy theo công thức, số vòng lặp của mình sẽ là khoảng 14 vòng lặp
s = 10
subset = np.array(random.sample(list(data), s))
X = np.expand_dims(subset[:,0],axis=1)
y = subset[:,1]
reg = LinearRegression().fit(X,y)
# reg.predict(X)
plt.scatter(data[:,0],data[:,1],s=20, marker = 'x')
plt.scatter(subset[:,0],subset[:,1],c='red',s=20)
plt.plot([[0],[100]],reg.predict([[0],[100]]),c='red')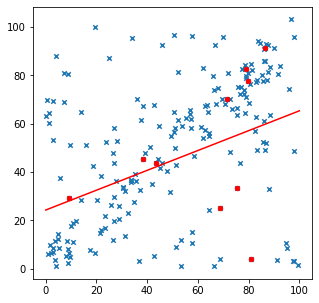
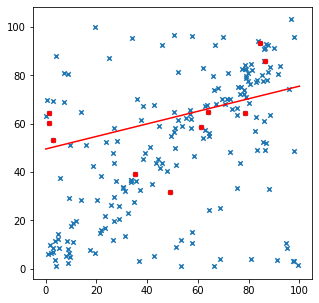
Sau đó, sử dụng mô hình tìm được để xác định các điểm đồng thuận
threshold = 15
consensus_count = 0
consensus = []
for points in data:
predict_value = reg.predict([[points[0]]])
#If predicted value is stay inside threshold, it's a consensus
if abs(predict_value - points[1]) < threshold:
consensus_count += 1
consensus.append(points)
consensus = np.array(consensus)
#Plot the regression line and the thresholds
plt.plot([[0],[100]],reg.predict([[0],[100]]),c='green')
plt.plot([[0],[100]],reg.predict([[0],[100]])+threshold,c='red')
plt.plot([[0],[100]],reg.predict([[0],[100]])-threshold,c='red')
#Plot data points
plt.scatter(data[:,0],data[:,1],s=20, marker = 'x')
plt.scatter(consensus[:,0],consensus[:,1],c='green', s=10)
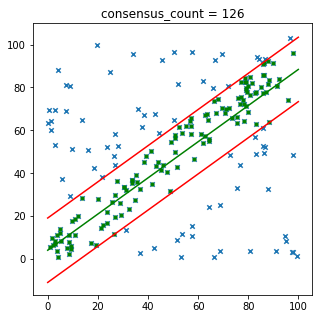
plt.title('consensus_count = '+str(consensus_count))
plt.show()
Sau 14 vòng lặp, mình tìm được mô hình có tỉ lệ đồng thuận cao nhất với 126 điểm đồng thuận, từ những điểm đồng thuận này, mình có thể xây dựng lại một mô hình mới với độ chính xác cao hơn.
4. Ứng dụng
Thuật toán RANSAC thường được sử dụng trong Computer Vision, ví dụ:
- Correspondence problem: Bài toán này giúp tìm ra các phần tương ứng nhau giữa 2 bức ảnh. Bài toán này lại liên quan và giải quyết nhiều vấn đề khác trong computer vision như Theo dõi vật thể (Object tracking), Camera chuyển động hay gần gũi nhất đó là thuật toán xây dựng ảnh panorama: ghép nhiều bức ảnh liền kề thành 1 bức ảnh dài

- Ước lượng ma trận cơ sở: ma trận cơ sở được sử dựng để hiện ma trận chuyển cơ sở giữa 2 không gian vectơ.
- khái niệm này lại liên quan đến rất nhiều vấn đề khác trong đó có việc xây dựng ảnh lập thể (ảnh từ stereo camera – tương tự như mắt người) Ảnh này tương tự như lúc bạn sử dụng kính thực tế ảo VR, mỗi bên kính sẽ render ra một ảnh tương ứng với những gì bạn nhìn thấy trong mắt trái/phải

- Vấn đề ảnh Cấu trúc từ chuyển động: Structure from motion (SfM): tạo ra mô hình 3D từ ảnh các vật thể di chuyển
- Scale-invariant feature transform: hay còn gọi là SIFT: nhận diện và khớp các thuộc tính giữa 2 bức ảnh

- Bài toán Xác định Vị trí (Location Determination Problem – LDP) như ở đầu bài mình có đề cập
- Còn tỉ tỉ những ứng dụng có liên quan tới computer vision mà có ứng dụng RANSAC nữa mà mình không kể hết 😀
Vậy các bạn đã biết RANSAC là gì rồi đúng không nào, đừng ngại tìm hiểu cách mà RANSAC được sử dụng vào bao la các ứng dụng khác trong computer vision, Cám ơn các bạn đã theo dõi.









bài viết hay, stay tuned!