Phát hiện bất thường là công việc tìm ra các điểm dữ liệu bị sai lệch so với tiêu chuẩn. Nói cách khác, đó là những điểm dữ liệu không tuân theo khuôn mẫu mong đợi. Outliers (các điểm ngoại vi) và exceptions (ngoại lệ) là các thuật ngữ được sử dụng để mô tả dữ liệu bất thường. Phát hiện bất thường rất quan trọng trong nhiều lĩnh vực vì nó cung cấp thông tin có giá trị và có thể đưa đến các hành động để xử lý. Ví dụ, một điểm bất thường trong quá trình quét ảnh MR có thể chỉ ra vùng có khối u trong não hay một kết quả bất thường từ cảm biến của nhà máy sản xuất có thể chỉ ra một bộ phận bị hỏng trong dây chuyền máy móc.

Bài viết này sẽ đi qua:
- Định nghĩa về khái niệm anomaly detection trong khai phá dữ liệu
- Một vài phương pháp nhanh để phát hiện bất thường trong dữ liệu
Anomaly Detection – Phát hiện bất thường?
Điểm ngoại lai (outliers) là các điểm dữ liệu sai lệch đáng kể so với phần còn lại của dữ liệu trong một tập dữ liệu cụ thể. Theo đó, phát hiện bất thường là quá trình xác định các điểm bất thường của dữ liệu hay các điểm ngoại lai.
Đối với các tập dữ liệu lớn, những outlier có thể bao gồm những dạng rất phức tạp mà không thể phát hiện bằng cách chỉ đơn giản nhìn vào dữ liệu. Vì vậy, khi triển khai ứng dụng machine learning thì việc nghiên cứu phát hiện dị thường có ý nghĩa rất lớn.
Các kiểu bất thường
Trong lĩnh vực khoa học dữ liệu, chúng ta có 3 cách khác nhau để phân loại các dị thường. Việc hiểu rõ chúng có thể có tác động lớn đến cách bạn xử lý các bất thường.
- Bất thường toàn cục (Global anomalies): các điểm dữ liệu khác biệt đáng kể so với phần còn lại của dữ liệu, dị thường toàn cục được biết đến là dạng dị thường phổ biến nhất. Thông thường, các điểm bất thường toàn cục có giá trị ở rất xa so với giá trị trung bình hoặc hoặc median của dữ liệu.
- Bất thường có điều kiện (Contextual or Conditional Anomalies): Những bất thường này có giá trị khác hẳn những điểm dữ liệu khác trong cùng 1 điều kiện. Ví dụ trong tập dữ liệu về giao dịch bán lẻ, một hóa đơn cho bàn chải đánh răng có giá 500.000đ sẽ là bất thường so với một hóa đơn bàn chải đánh răng thông thường, mặc dù hóa đơn trị giá 500.000đ vẫn phổ biến trong tất cả các hóa đơn
- Bất thường tập thể (Collective Anomalies): là bất thường xảy ra khi một tập hợp các điểm dữ liệu gây ra hiện tượng bất thường. Các điểm dữ liệu riêng lẻ trong một bất thường tập thể có thể không phải là bất thường, nhưng sự xuất hiện của chúng cùng nhau dưới dạng một tập hợp là bất thường. Ví dụ, nhịp tim của một người có thể nằm trong khoảng từ 50 đến 150 BPM, nhưng một tập dữ liệu về nhịp tim của một nhóm người mình thường bỗng nhiên xuất hiện một nhóm record mang giá trị 150BPM, thì đó được xem là 1 tập hợp bất thường
Có rất nhiều phương pháp được sử dụng để phát hiện sự bất thường, nhưng chúng ta hãy triển khai một vài phương pháp để hiểu cách chúng được sử dụng cho các trường hợp sử dụng khác nhau. Ở đây mình giới thiệu 2 phương pháp là Isolation Forest và Kernel Density Estimation
Isolation Forest
Cũng như random forests, isolation forests được xây dựng từ cây quyết định – decision tree. Thuật toán này được triển khai theo hướng không giám sát, do đó sẽ không cần phải được gắn nhãn trước. Isolation forests được thiết kế dựa trên ý tưởng: nhiễu là những thành phần “có ít và duy nhất” trong tập dữ liệu.
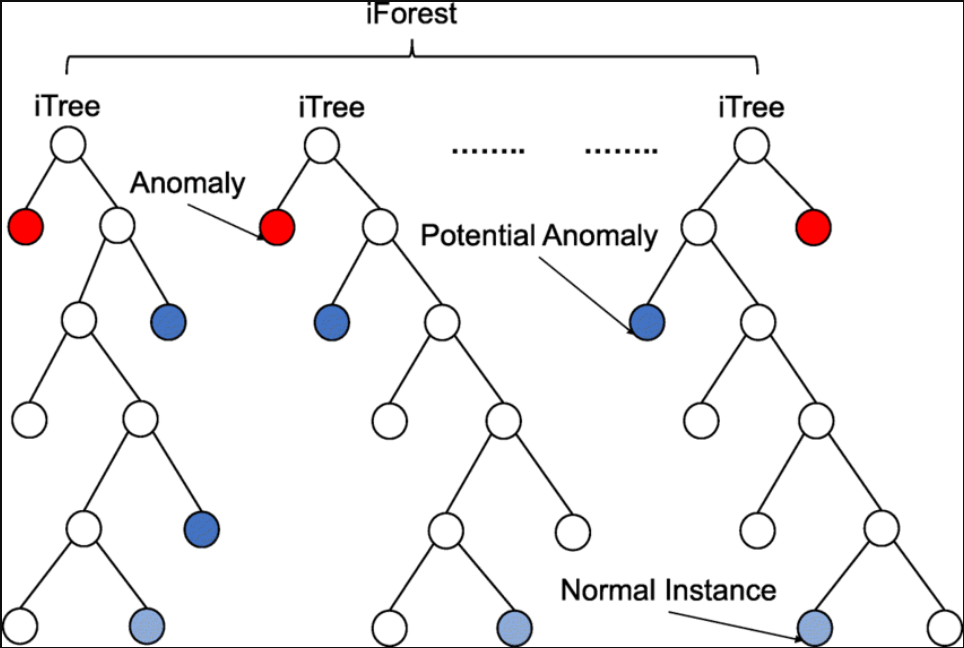
Nhắc lại, cây quyết định được xây dựng dựa trên những thông tin tiêu chuẩn như chỉ số Gini hoặc entropy. Những nhóm có đặc điểm khác nhau sẽ được rẽ ra từ gốc của cây quyết định, và tiếp tục rẽ ra những nhánh khác nhau nữa dựa trên những đặc điểm phân biệt nhỏ hơn. Nhờ vào việc các đặc điểm được lựa chọn ngẫu nhiên, isolation forest phân nhóm dữ liệu một cách ngẫu nhiên theo cấu trúc cây. Những điểm dữ liệu mà cần nhiều điều kiện hơn để phân định (rẽ nhánh nhiều hơn) chứng tỏ có xác suất rất nhỏ những điểm dữ liệu đó là nhiễu. Ngược lại, những điểm dữ liệu cần ít điều kiện để xác định (rẽ nhánh ít) thì có khả năng đó là những dữ liệu bất thường, bởi vì ta có thể nhận biết chúng 1 cách dễ dàng giữa rất nhiều điểm dữ liệu khác.
Mình sẽ cho các bạn một ví dụ với Python cho thấy thuật toán này hoạt động như thế nào.
from sklearn.datasets import make_blobs
import numpy as np
from sklearn.ensemble
import IsolationForest
import matplotlib.pyplot as pltChuẩn bị dữ liệu
Trước tiên, chúng ta tạo một cụm dữ liệu gồm 300 điểm, phân phối xung quanh điểm (10,10) với độ lệch chuẩn 0.3
np.random.seed(3)
X, _ = make_blobs(n_samples=300, centers=1, cluster_std=.3, center_box=(10, 10))
plt.scatter(X[:, 0], X[:, 1], marker="o", c=_, s=25, edgecolor="k")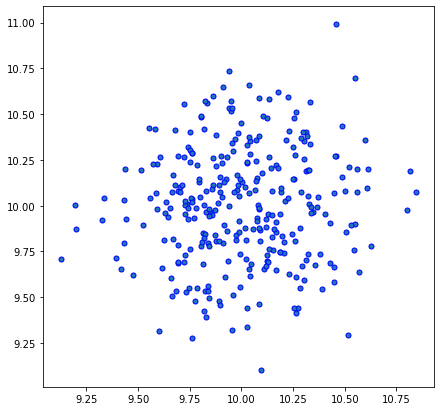
Để kết quả ro ràng hơn, mình quyết định tạo thêm vài điểm bất thường xung quanh (11,11)
random.seed(3)
X, _ = make_blobs(n_samples=300, centers=1, cluster_std=.3, center_box=(10,10))
outliers, _ = make_blobs(n_samples=10, centers=1, cluster_std=.05, center_box=(11,11))
X = np.concatenate([X,outliers])
plt.figure(figsize=(7,7))
plt.scatter(X[:, 0], X[:, 1], marker="o", s=25, edgecolor="b")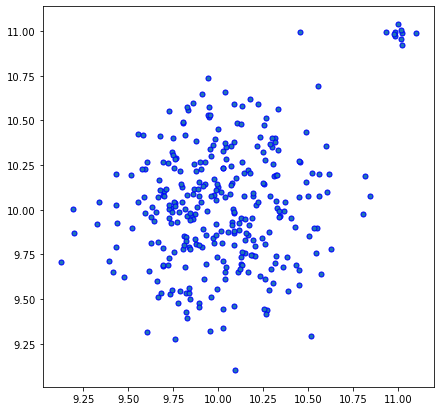
Xây dựng mô hình Isolation Forest Model cho tập dữ liệu
Ở đây, mình sẽ không xây dựng thuật toán từ đầu mà sử dụng class IsolationForest từ thư viện scikit-learn. Ở đây mình khởi tạo n_estimators cho khu rừng của mình là 100 (có thể ít hơn tùy bạn), và contamination – độ ô nhiễm là 0.05 (nếu không thể xác định, tốt nhất hãy để “auto”). Sau đó fit_predict() mô hình với dữ liệu đã cho.
IF = IsolationForest(n_estimators=100, contamination=.03)
predictions = IF.fit_predict(X)Những giá trị ngoại lai được xác định sẽ được gán label là -1.
outlier_index = np.where(predictions==-1)
values = X[outlier_index]
plt.scatter(X[:,0], X[:,1])
plt.scatter(values[:,0], values[:,1], color='y')
plt.show()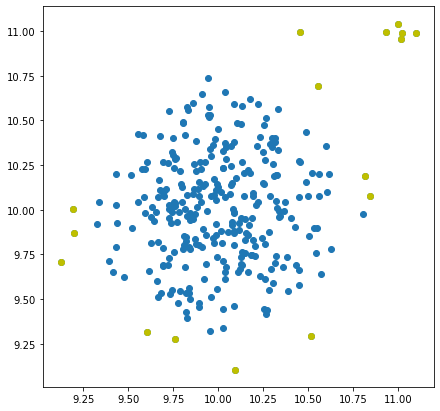
Như ta thấy, thuật toán isolation forest hoạt động khá tốt với dữ liệu mà chúng ta tạo ra.
Đây là toàn bộ code mà mình sử dụng:
from sklearn.datasets import make_blobs
import numpy as np
from sklearn.ensemble import IsolationForest
import matplotlib.pyplot as plt
np.random.seed(3)
X, _ = make_blobs(n_samples=300, centers=1, cluster_std=.3, center_box=(10,10))
outliers, _ = make_blobs(n_samples=5, centers=1, cluster_std=.05, center_box=(11,11))
X = np.concatenate([X,outliers])
plt.figure(figsize=(7,7))
plt.scatter(X[:, 0], X[:, 1], marker="o", s=25, edgecolor="b")
IF = IsolationForest(n_estimators=100, contamination=.05)
predictions = IF.fit_predict(X)
outlier_index = np.where(predictions==-1)
values = X[outlier_index]
plt.figure(figsize=(7,7))
plt.scatter(X[:,0], X[:,1], s=25, marker="o", edgecolor = 'b')
plt.scatter(values[:,0], values[:,1], s=25, marker="o", color='r')
plt.show()Kernel Density Estimation
Nếu thông thường, một tập dữ liệu chuẩn phải tuân theo một loại phân phối xác suất nhất định, thì các điểm bất thường hay ngoại lai là những điểm hiếm khi xuất hiện và không tuân theo phân phối xác suất. Kernel Density Estimation là một kỹ thuật ước tính hàm mật độ xác suất của các điểm dữ liệu một cách ngẫu nhiên trong không gian mẫu. Với hàm mật độ, chúng ta có thể phát hiện những điểm bất thường trong một tập dữ liệu bằng cách tìm ra những điểm không tuân theo phân phối xác suất của số đông.
Ý tưởng thuật toán này khá đơn giản, mình sẽ giải thích về phương pháp xây dựng Kernel Density Estimation trong một bài viết khác chi tiết hơn. Trong bài viết này, mình chỉ giới thiệu về phương pháp ứng dụng KDE trong dataset.
Tương tự như ứng dụng ở trên, ta cũng tạo ra một vài phân phối chuẩn kèm theo một vài điểm bất thường và sử dụng class KernelDensity từ scikit-learn để xác định outliers.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import KernelDensity
from sklearn.preprocessing import scaleXây dựng dữ liệu mẫu
np.random.seed(10)
X, _= make_blobs(n_features=2, centers=3, n_samples=500, cluster_std=2)
plt.figure(figsize=(7,7))
plt.scatter(X[:, 0], X[:, 1], marker="o", s=25, edgecolor="b")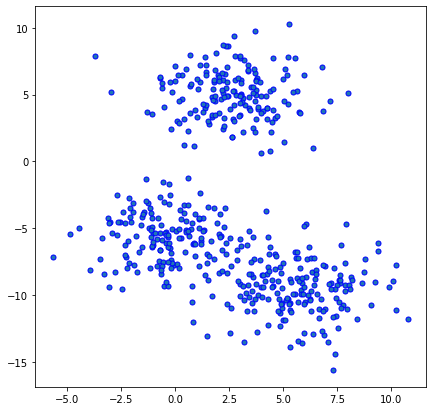
Prepare and Fit the Kernel Density Function for Prediction
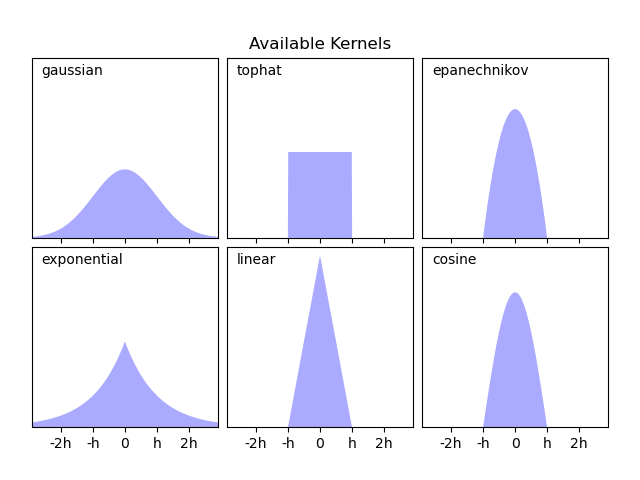
Sở dĩ mình lựa chọn kernel gaussian bởi vì mình đã tạo dataset dựa trên phân phối chuẩn, tùy thuộc vào nhận định của bạn về phân phối của dữ liệu, hãy lựa chọn kernel tương ứng
from sklearn.neighbors import KernelDensity
# Estimate density with a Gaussian kernel density estimator
kde = KernelDensity(kernel='gaussian')
kde.fit(X)Đoạn code dưới đây mình sử dụng để biểu diễn phân phối từ KDE của mình
x = X[:,0]
y = X[:,1]
xx, yy = np.mgrid[x.min():x.max():100j, y.min():y.max():100j]
positions = np.vstack([xx.ravel(), yy.ravel()])
zz = np.reshape(np.exp(kde.score_samples(positions.T)), xx.shape)
plt.figure(figsize=(7,7))
plt.imshow(np.rot90(Z), extent=[x.min(), x.max(), y.min(), y.max()])
plt.scatter(x, y, s=5,edgecolor='w')
plt.show()
KernelDensity có chứa phương thức score_sample() giúp bạn tính toán log-likelihood của những điểm dữ liệu trong dataset của bạn so với phân phối tính được (log Likely-hood estimation). Bằng cách này, chúng ta có thể sử dụng quantile() kèm theo một ngưỡng phù hợp để lấy ra những điểm ít phù hợp nhất với phân phối KDE.
kde_X = kde.score_samples(X)
contamination = 0.05
tau_kde = np.quantile(kde_X, contamination)
outliers_arg = np.argwhere(kde_X < tau_kde)
outliers_arg = outliers.flatten()
outliers = X[outliers_arg]
normal_samples = np.argwhere(kde_X >= tau_kde)
normal_samples = normal_samples.flatten()
X_valid = X[normal_samples]Ở đây mình chọn contamination = 0.05 có nghĩa là mình đã ước lượng outliers sẽ chiếm 5% trong tổng số dữ liệu.
plt.figure(figsize=(7,7))
plt.scatter(X_valid[:, 0], X_valid[:, 1], c="tab:green", label="Valid Samples")
plt.scatter(X_outliers[:, 0], X_outliers[:, 1], c="tab:red", label="Outliers")
plt.show()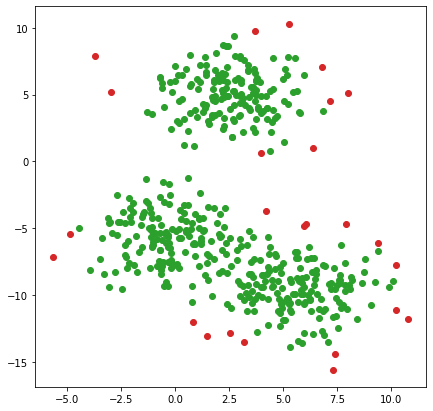
Tương tự Isolation Forest, Anomalies detecting dựa trên KDE cũng hoạt động rất tốt trên dữ liệu mình tạo ra.
Đây là toàn bộ code mình sử dụng:
np.random.seed(10)
X, _= make_blobs(n_features=2, centers=3, n_samples=500, cluster_std=2)
plt.figure(figsize=(7,7))
plt.scatter(X[:, 0], X[:, 1], marker="o", s=25, edgecolor="b")
kde = KernelDensity(kernel='gaussian').fit(X)
x, y = X[:,0], X[:,1]
xx, yy = np.mgrid[x.min():x.max():100j, y.min():y.max():100j]
positions = np.vstack([xx.ravel(), yy.ravel()])
zz = np.reshape(np.exp(kde.score_samples(positions.T)), xx.shape)
plt.figure(figsize=(7,7))
plt.imshow(np.rot90(Z), extent=[x.min(), x.max(), y.min(), y.max()])
plt.scatter(x, y, s=5,edgecolor='w')
plt.show()
kde_X = kde.score_samples(X)
contamination = 0.05
tau_kde = np.quantile(kde_X, contamination)
outliers = np.argwhere(kde_X < tau_kde)
outliers = outliers.flatten()
X_outliers = X[outliers]
normal_samples = np.argwhere(kde_X >= tau_kde)
normal_samples = normal_samples.flatten()
X_valid = X[normal_samples]
plt.figure(figsize=(7,7))
plt.scatter(X_valid[:, 0], X_valid[:, 1], marker="o", s=25, edgecolor="b", label="Valid Samples")
plt.scatter(X_outliers[:, 0], X_outliers[:, 1], label="Outliers")
plt.show()









Blog trông thú vị phết