Manifold Learning: “HELLO”¶
Để làm cho những khái niệm này rõ ràng hơn, hãy bắt đầu bằng việc tạo ra một số dữ liệu hai chiều mà chúng ta có thể sử dụng để xác định một không gian nhất định.Đây là một hàm sẽ tạo ra dữ liệu theo hình dạng của từ “HELLO”:
def make_hello(N=1000, rseed=42): # Make a plot with "HELLO" text; save as PNG fig, ax = plt.subplots(figsize=(4, 1)) fig.subplots_adjust(left=0, right=1, bottom=0, top=1) ax.axis('off') ax.text(0.5, 0.4, 'HELLO', va='center', ha='center', weight='bold', size=85) fig.savefig('hello.png') plt.close(fig) # Open this PNG and draw random points from it from matplotlib.image import imread data = imread('hello.png')[::-1, :, 0].T rng = np.random.RandomState(rseed) X = rng.rand(4 * N, 2) i, j = (X * data.shape).astype(int).T mask = (data[i, j] < 1) X = X[mask] X[:, 0] *= (data.shape[0] / data.shape[1]) X = X[:N] return X[np.argsort(X[:, 0])]
Hãy gọi hàm và hiển thị dữ liệu kết quả:
X = make_hello(1000)colorize = dict(c=X[:, 0], cmap=plt.cm.get_cmap('rainbow', 5))plt.scatter(X[:, 0], X[:, 1], **colorize)plt.axis('equal');
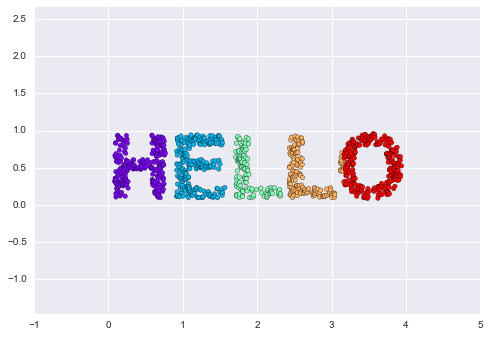
Kết quả đầu ra là hai chiều và bao gồm các điểm được vẽ theo hình dạng của từ “HELLO”.Hình dạng dữ liệu này sẽ giúp chúng ta nhìn thấy một cách hình dung những thuật toán này đang làm gì.
Phân tích đa chiều (MDS)¶
Nhìn vào dữ liệu như thế này, chúng ta có thể thấy rằng lựa chọn cụ thể của các giá trị x và y của tập dữ liệu không phải là mô tả cơ bản nhất về dữ liệu: chúng ta có thể tỉ lệ, co lại hoặc xoay dữ liệu và “HELLO” vẫn hiển thị rõ ràng.
def rotate(X, angle): theta = np.deg2rad(angle) R = [[np.cos(theta), np.sin(theta)], [-np.sin(theta), np.cos(theta)]] return np.dot(X, R) X2 = rotate(X, 20) + 5plt.scatter(X2[:, 0], X2[:, 1], **colorize)plt.axis('equal');
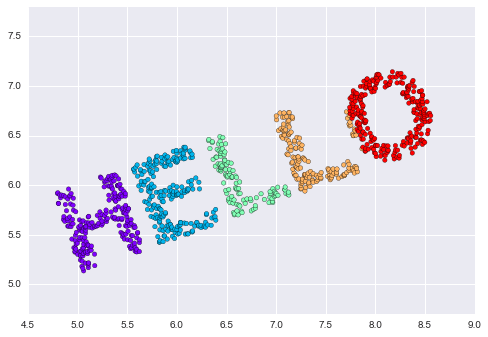
Điều này cho chúng ta biết rằng các giá trị x và y không nhất thiết phải là các yếu tố cơ bản trong các mối quan hệ trong dữ liệu.Những gì cơ bản, trong trường hợp này, là khoảng cách giữa mỗi điểm và các điểm khác trong tập dữ liệu.Một cách phổ biến để biểu diễn điều này là sử dụng ma trận khoảng cách: cho $N$ điểm, chúng ta xây dựng một mảng $N \times N$ sao cho mục $(i, j)$ chứa khoảng cách giữa điểm $i$ và điểm $j$.Hãy sử dụng hàm pairwise_distances hiệu quả của Scikit-Learn để làm điều này cho dữ liệu gốc của chúng ta:
from sklearn.metrics import pairwise_distancesD = pairwise_distances(X)D.shape
(1000, 1000)
Như đã hứa, với điểm N=1.000 của chúng ta, chúng ta thu được một ma trận 1000×1000, có thể được visualized như được hiển thị ở đây:
plt.imshow(D, zorder=2, cmap='Blues', interpolation='nearest')plt.colorbar();
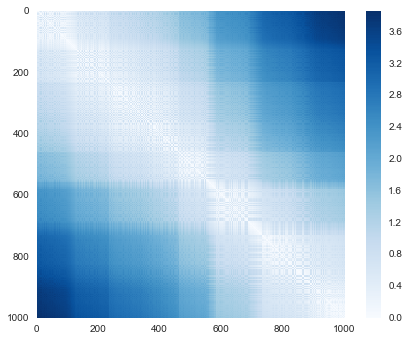
Nếu chúng ta tương tự xây dựng ma trận khoảng cách cho dữ liệu đã được xoay và dịch, chúng ta sẽ thấy rằng nó giống nhau:
D2 = pairwise_distances(X2)np.allclose(D, D2)
True
Ma trận khoảng cách này cung cấp cho chúng ta một biểu diễn của dữ liệu mà không thay đổi sau khi xoay và dịch chuyển, nhưng biểu đồ của ma trận trên không hoàn toàn dễ hiểu.
Tiếp theo, trong khi tính toán ma trận khoảng cách này từ các tọa độ (x, y) là đơn giản, việc chuyển đổi lại các khoảng cách thành tọa độ x và y là khá khó khăn.Đây chính là mục tiêu của thuật toán scaling đa chiều: với một ma trận khoảng cách giữa các điểm, nó khôi phục lại một biểu diễn tọa độ $D$ chiều của dữ liệu.Hãy xem làm thế nào nó hoạt động với ma trận khoảng cách của chúng ta, sử dụng precomputed dissimilarity để chỉ định rằng chúng ta đang truyền một ma trận khoảng cách:
from sklearn.manifold import MDSmodel = MDS(n_components=2, dissimilarity='precomputed', random_state=1)out = model.fit_transform(D)plt.scatter(out[:, 0], out[:, 1], **colorize)plt.axis('equal');
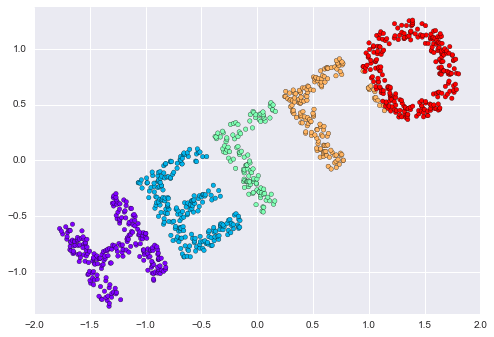
Thuật toán MDS khôi phục một trong hai biểu diễn tọa độ hai chiều có thể của dữ liệu của chúng ta, chỉ sử dụng ma trận khoảng cách $N\times N$ miêu tả mối quan hệ giữa các điểm dữ liệu.
MDS như một phương pháp Học không gian con¶
Điều hữu ích của việc này trở nên rõ ràng hơn khi chúng ta xem xét điều kiện rằng ma trận khoảng cách có thể được tính toán từ dữ liệu trong bất kỳ chiều nào.Vì vậy, ví dụ, thay vì chỉ đơn giản xoay dữ liệu trong mặt phẳng hai chiều, chúng ta có thể chiếu nó vào ba chiều bằng cách sử dụng hàm sau đây (về cơ bản là một sự tổng quát ba chiều của ma trận xoay được sử dụng trước đó):
def random_projection(X, dimension=3, rseed=42): assert dimension >= X.shape[1] rng = np.random.RandomState(rseed) C = rng.randn(dimension, dimension) e, V = np.linalg.eigh(np.dot(C, C.T)) return np.dot(X, V[:X.shape[1]]) X3 = random_projection(X, 3)X3.shape
(1000, 3)
Hãy trực quan hóa những điểm này để hiểu được chúng ta đang làm việc với những gì:
from mpl_toolkits import mplot3dax = plt.axes(projection='3d')ax.scatter3D(X3[:, 0], X3[:, 1], X3[:, 2], **colorize)ax.view_init(azim=70, elev=50)
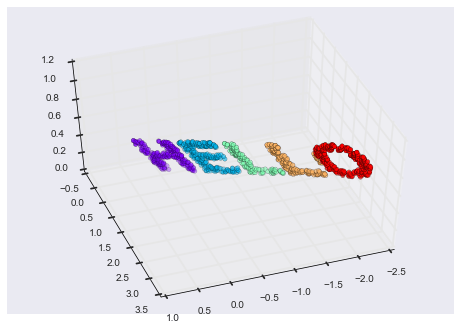
Bây giờ chúng ta có thể yêu cầu bộ ước lượng MDS nhập dữ liệu ba chiều này, tính ma trận khoảng cách, và sau đó xác định phép nhúng hai chiều tối ưu cho ma trận khoảng cách này.Kết quả khôi phục lại một biểu diễn của dữ liệu ban đầu:
model = MDS(n_components=2, random_state=1)out3 = model.fit_transform(X3)plt.scatter(out3[:, 0], out3[:, 1], **colorize)plt.axis('equal');
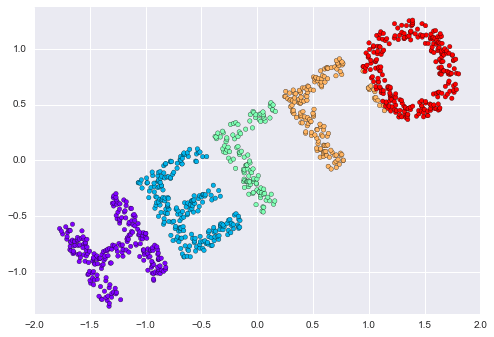
Đây chủ yếu là mục tiêu của một bộ ước lượng manifold learning: với dữ liệu nhúng nhiều chiều, nó tìm kiếm một biểu diễn ít chiều của dữ liệu sao cho giữ được một số mối quan hệ trong dữ liệu.Trong trường hợp của MDS, lượng được giữ lại là khoảng cách giữa mỗi cặp điểm.
Mô hình Nhúng Phi tuyến: Nơi MDS Thất bại¶
Cuộc thảo luận của chúng ta cho đến nay đã xem xét các nhúng tuyến tính, tức là bao gồm việc xoay, dịch và tỉ lệ của dữ liệu vào không gian có số chiều cao hơn.Ở đây MDS không thành công khi nhúng là phi tuyến—nghĩa là khi nó vượt ra khỏi bộ phép thủ công đơn giản này.Hãy xem xét sự nhúng sau đây, nó chuyển đổi đầu vào và uốn cong nó thành hình chữ “S” trong ba chiều:
def make_hello_s_curve(X): t = (X[:, 0] - 2) * 0.75 * np.pi x = np.sin(t) y = X[:, 1] z = np.sign(t) * (np.cos(t) - 1) return np.vstack((x, y, z)).TXS = make_hello_s_curve(X)
Đây là dữ liệu ba chiều một lần nữa, nhưng chúng ta có thể thấy rằng việc nhúng này phức tạp hơn nhiều:
from mpl_toolkits import mplot3dax = plt.axes(projection='3d')ax.scatter3D(XS[:, 0], XS[:, 1], XS[:, 2], **colorize);
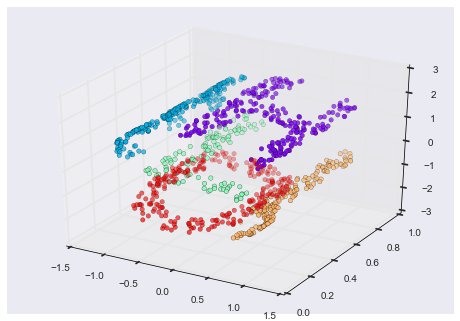
Các mối quan hệ cơ bản giữa các điểm dữ liệu vẫn tồn tại, nhưng lần này dữ liệu đã được biến đổi theo một cách phi tuyến: nó đã được gói gọn trong hình dạng của chữ “S”.
Nếu chúng ta thử một thuật toán MDS đơn giản trên dữ liệu này, nó sẽ không thể “giải nén” được nhúng không tuyến tính này, và chúng ta mất đi sự theo dõi các mối quan hệ cơ bản trong không gian nhúng:
from sklearn.manifold import MDSmodel = MDS(n_components=2, random_state=2)outS = model.fit_transform(XS)plt.scatter(outS[:, 0], outS[:, 1], **colorize)plt.axis('equal');
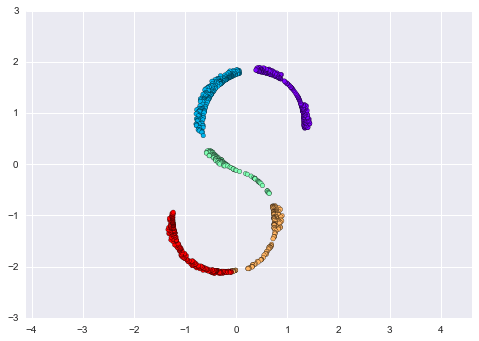
Phương pháp nhúng tuyến tính hai chiều tốt nhất không giải quyết vấn đề gỡ bỏ S-curve, mà thay vào đó bỏ đi trục y ban đầu.
Manifold phi tuyến: Nhúng tuyến tính cục bộ¶
Làm thế nào chúng ta có thể tiến xa ở đây? Nhìn từ xa, chúng ta có thể nhận thấy rằng nguồn gốc của vấn đề là MDS cố gắng bảo tồn các khoảng cách giữa các điểm cách xa nhau khi xây dựng embedding.Nhưng nếu chúng ta sửa đổi thuật toán sao cho nó chỉ bảo tồn khoảng cách giữa các điểm gần nhau thì embedding kết quả sẽ gần hơn với những gì chúng ta muốn.
Mô hình này có thể được mô tả như hình minh họa dưới đây:
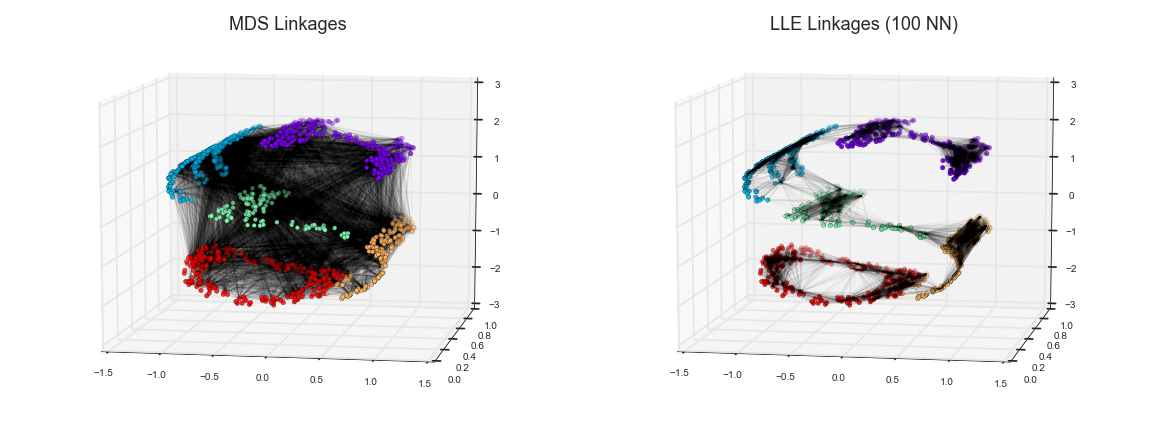
Ở đây, mỗi đường kẻ nhạt đại diện cho một khoảng cách cần được bảo toàn trong việc nhúng.Ấn tượng bên trái là mô hình được sử dụng bởi MDS: nó cố gắng bảo toàn các khoảng cách giữa mỗi cặp điểm trong tập dữ liệu.Ấn tượng bên phải là mô hình được sử dụng bởi một thuật toán học gọn các đường thẳng gọi là locally linear embedding (LLE): thay vì bảo toàn tất cả các khoảng cách, nó thay vào đó cố gắng bảo toàn chỉ khoảng cách giữa các điểm lân cận: trong trường hợp này, số lân cận gần nhất của mỗi điểm là 100.
Trong suy nghĩ về bảng điều khiển bên trái, chúng ta có thể thấy tại sao MDS (Multi-Dimensional Scaling) thất bại: không có cách nào để làm phẳng dữ liệu này trong khi vẫn bảo tồn đúng đắn độ dài của mỗi đường vẽ giữa hai điểm.Đối với bảng điều khiển bên phải, thì nhìn chung, mọi thứ trông lạc quan hơn một chút. Chúng ta có thể tưởng tượng việc gỡ bo dữ liệu theo cách mà vẫn giữ nguyên độ dài của các đường vẽ xấp xỉ nhau.Đó chính xác là những gì LLE (Locally Linear Embedding) làm, thông qua tối ưu hóa toàn cầu của một hàm chi phí phản ánh logic này.
LLE có một số phiên bản khác nhau; ở đây chúng ta sẽ sử dụng thuật toán LLE đã được sửa đổi để khôi phục lại mặt phẳng hai chiều được nhúng.Nói chung, LLE đã được sửa đổi hoạt động tốt hơn so với các phiên bản khác của thuật toán để khôi phục những mặt phẳng xác định tốt với sự méo mó ít:
from sklearn.manifold import LocallyLinearEmbeddingmodel = LocallyLinearEmbedding(n_neighbors=100, n_components=2, method='modified', eigen_solver='dense')out = model.fit_transform(XS)fig, ax = plt.subplots()ax.scatter(out[:, 0], out[:, 1], **colorize)ax.set_ylim(0.15, -0.15);
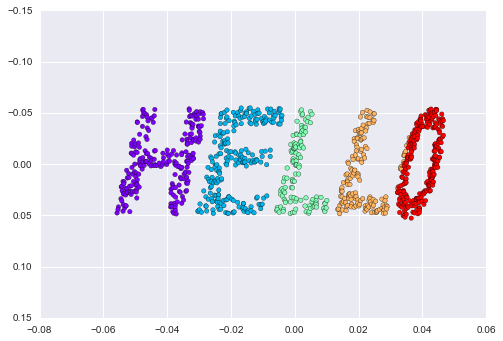
Kết quả vẫn có phần bị méo so với manifold ban đầu của chúng ta, nhưng vẫn bắt lấy được những mối quan hệ cốt yếu trong dữ liệu!
Nhận định về phương pháp Manifold¶
Mặc dù câu chuyện và động lực này hấp dẫn, trong thực tế, các kỹ thuật manifold learning thường khá khó tính toán đối với việc sử dụng chúng cho nhiều mục đích khác nhau ngoài việc trực quan hóa định tính đơn giản của dữ liệu nhiều chiều.
Có những thách thức đặc biệt sau đây của phân loại không gian đơn, mà tất cả đều không tốt hơn so với PCA:
- Trong phân loại không gian, không có một khung để xử lý dữ liệu bị thiếu tốt. Ngược lại, có các phương pháp lặp để xử lý dữ liệu bị thiếu trong PCA.
- Trong phân loại không gian, sự hiện diện của nhiễu trong dữ liệu có thể “tắt” ngắn mạch không gian và thay đổi nhúng một cách đáng kể. Ngược lại, PCA tự động lọc nhiễu từ các thành phần quan trọng nhất.
- Kết quả nhúng không gian phụ thuộc rất nhiều vào số hàng xóm được chọn và không có cách định lượng cụ thể để chọn số hàng xóm tối ưu. Ngược lại, PCA không liên quan đến sự lựa chọn này.
- Trong phân loại không gian, việc xác định số chiều đầu ra tối ưu theo toàn cầu là khó khăn. Ngược lại, PCA cho phép bạn tìm số chiều đầu ra dựa trên phương sai được giải thích.
- Trong phân loại không gian, ý nghĩa của các chiều nhúng không luôn rõ ràng. Trong PCA, các thành phần chính có ý nghĩa rõ ràng.
- Trong phân loại không gian, chi phí tính toán của các phương pháp không gian phụ thuộc vào O[N^2] hoặc O[N^3]. Đối với PCA, có các phương pháp ngẫu nhiên tồn tại mà thường nhanh hơn nhiều (mặc dù xem gói megaman để biết thêm các cài đặt có thể mở rộng hơn của phân loại không gian).
Với tất cả những thông tin trên bàn, ưu điểm duy nhất rõ ràng của các phương pháp manifold learning so với PCA là khả năng giữ nguyên mối quan hệ phi tuyến trong dữ liệu; vì lý do đó, tôi thường khám phá dữ liệu với các phương pháp manifold chỉ sau khi đã khám phá chúng với PCA trước đó.
Scikit-Learn thực hiện một số biến thể phổ biến của việc học đa chiều ngoài Isomap và LLE: tài liệu của Scikit-Learn có một thảo luận tuyệt vời và so sánh về chúng.Dựa trên kinh nghiệm của riêng tôi, tôi sẽ đưa ra các khuyến nghị sau:
- Đối với các bài toán giả định như đường cong S mà chúng ta đã thấy trước đó, nhúng cục bộ tuyến tính (LLE) và các biến thể của nó (đặc biệt là LLE sửa đổi), hoạt động rất tốt. Điều này được thực hiện trong
sklearn.manifold.LocallyLinearEmbedding. - Đối với dữ liệu cao chiều từ các nguồn thực tế, LLE thường sản sinh kết quả kém và ánh xạ cùng đẳng (IsoMap) dường như dẫn đến nhúng ý nghĩa hơn. Điều này được thực hiện trong
sklearn.manifold.Isomap - Đối với dữ liệu có tính gom cụm cao, t-distributed stochastic neighbor embedding (t-SNE) dường như hoạt động rất tốt, mặc dù có thể chậm hơn so với các phương pháp khác. Điều này được thực hiện trong
sklearn.manifold.TSNE.
Nếu bạn quan tâm và muốn hiểu cách chúng hoạt động, tôi đề xuất bạn chạy từng phương thức trên dữ liệu trong phần này.
Ví dụ: Isomap trên Khuôn mặt¶
Một nơi mà manifold learning thường được sử dụng là trong việc hiểu quan hệ giữa các điểm dữ liệu có số chiều cao.Một trường hợp phổ biến của dữ liệu có số chiều cao là hình ảnh: ví dụ, một tập hình ảnh với 1.000 pixel mỗi hình ảnh có thể được coi như một tập điểm trong 1.000 chiều – độ sáng của mỗi pixel trong mỗi hình ảnh xác định tọa độ trong chiều đó.
Ở đây chúng ta sẽ áp dụng Isomap trên một số dữ liệu khuôn mặt.Chúng ta sẽ sử dụng bộ dữ liệu Labeled Faces in the Wild, mà chúng ta đã từng thấy trong In-Depth: Support Vector Machines và In Depth: Principal Component Analysis.Chạy lệnh này sẽ tải xuống dữ liệu và lưu vào thư mục home của bạn để sử dụng sau này:
from sklearn.datasets import fetch_lfw_peoplefaces = fetch_lfw_people(min_faces_per_person=30)faces.data.shape
(2370, 2914)
Chúng ta có 2.370 hình ảnh, mỗi hình ảnh có 2.914 điểm ảnh.Nói cách khác, chúng ta có thể coi các hình ảnh như các điểm dữ liệu trong một không gian 2.914 chiều!\<\/p>
Hãy nhanh chóng minh họa một số hình ảnh này để xem chúng ta đang làm việc với gì:
fig, ax = plt.subplots(4, 8, subplot_kw=dict(xticks=[], yticks=[]))for i, axi in enumerate(ax.flat): axi.imshow(faces.images[i], cmap='gray')

Chúng tôi muốn vẽ một khối nhúng chiều thấp của dữ liệu 2,914 chiều để tìm hiểu mối quan hệ cơ bản giữa các hình ảnh.Một cách hữu ích để bắt đầu là tính toán một PCA và xem tỷ lệ phương sai được giải thích, điều này sẽ cho chúng ta một ý tưởng về số lượng đặc trưng tuyến tính cần thiết để mô tả dữ liệu:
from sklearn.decomposition import RandomizedPCAmodel = RandomizedPCA(100).fit(faces.data)plt.plot(np.cumsum(model.explained_variance_ratio_))plt.xlabel('n components')plt.ylabel('cumulative variance');
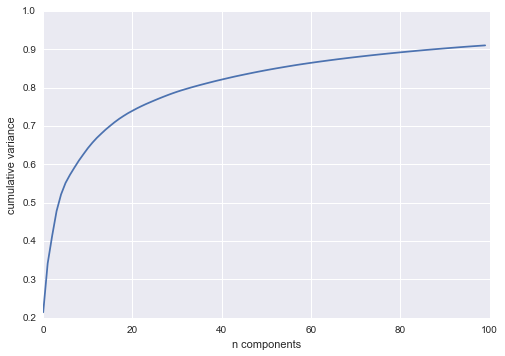
Ta thấy rằng với tập dữ liệu này, gần 100 thành phần được yêu cầu để bảo tồn 90% phương sai: điều này cho chúng ta biết rằng dữ liệu có chiều cao cơ bản – nó không thể được mô tả một cách tuyến tính chỉ với một vài thành phần.
Khi trường hợp này xảy ra, việc nhúng không gian phi tuyến như LLE và Isomap có thể hữu ích.Chúng ta có thể tính toán việc nhúng Isomap trên những khuôn mặt này bằng cách sử dụng mẫu giống như đã được hiển thị trước đó:
from sklearn.manifold import Isomapmodel = Isomap(n_components=2)proj = model.fit_transform(faces.data)proj.shape
(2370, 2)
Kết quả là một chiếu hai chiều của tất cả các hình ảnh đầu vào.Để hiểu rõ hơn về những thông tin mà chiếu hai chiều cung cấp cho chúng ta, hãy xác định một hàm sẽ xuất ra các hình thu nhỏ tại vị trí của các chiếu:
from matplotlib import offsetboxdef plot_components(data, model, images=None, ax=None, thumb_frac=0.05, cmap='gray'): ax = ax or plt.gca() proj = model.fit_transform(data) ax.plot(proj[:, 0], proj[:, 1], '.k') if images is not None: min_dist_2 = (thumb_frac * max(proj.max(0) - proj.min(0))) ** 2 shown_images = np.array([2 * proj.max(0)]) for i in range(data.shape[0]): dist = np.sum((proj[i] - shown_images) ** 2, 1) if np.min(dist) < min_dist_2: # don't show points that are too close continue shown_images = np.vstack([shown_images, proj[i]]) imagebox = offsetbox.AnnotationBbox( offsetbox.OffsetImage(images[i], cmap=cmap), proj[i]) ax.add_artist(imagebox)
Gọi hàm này ngay bây giờ, chúng ta sẽ thấy kết quả:
fig, ax = plt.subplots(figsize=(10, 10))plot_components(faces.data, model=Isomap(n_components=2), images=faces.images[:, ::2, ::2])
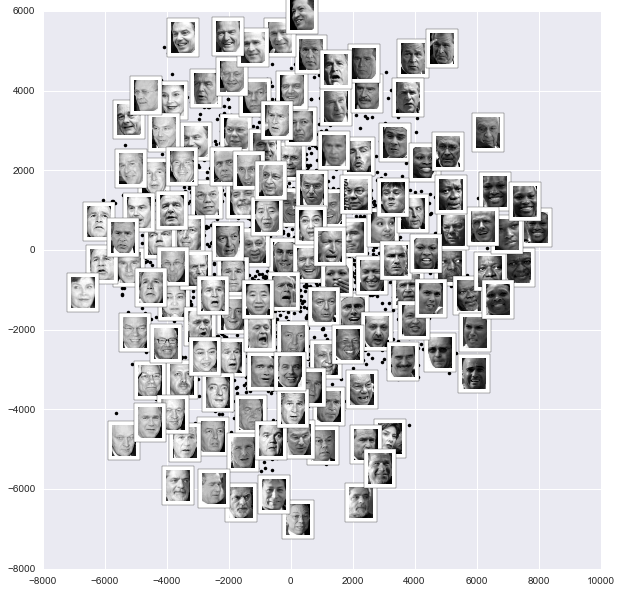
Kết quả là thú vị: hai chiều đầu tiên của Isomap dường như mô tả các đặc trưng toàn cầu của hình ảnh: sự tối hoặc sáng chung của hình ảnh từ trái sang phải, và định hướng chung của khuôn mặt từ dưới lên trên.Điều này mang lại cho chúng ta một chỉ định trực quan đẹp về một số đặc điểm cơ bản trong dữ liệu của chúng ta.
Chúng ta có thể tiếp tục phân loại dữ liệu này (có thể sử dụng các đặc trưng manifold như đầu vào cho thuật toán phân loại) như chúng ta đã làm trong In-Depth: Support Vector Machines.
Ví dụ: Hiển thị cấu trúc trong chữ số¶
Như một ví dụ khác về việc sử dụng manifold learning để trực quan hóa, hãy cùng nhìn vào tập dữ liệu MNIST các chữ số viết tay.Dữ liệu này tương tự như những chữ số chúng ta đã thấy trong In-Depth: Cây quyết định và Rừng ngẫu nhiên, nhưng với nhiều pixel hơn trong mỗi hình ảnh.Nó có thể được tải xuống từ http://mldata.org/ bằng công cụ Scikit-Learn:
from sklearn.datasets import fetch_mldatamnist = fetch_mldata('MNIST original')mnist.data.shape
(70000, 784)
Đoạn mã HTML này bao gồm 70.000 hình ảnh, mỗi hình ảnh có 784 điểm ảnh (tức là hình ảnh có kích thước 28×28).Tương tự như trước đây, chúng ta có thể nhìn vào một số hình ảnh đầu tiên:
fig, ax = plt.subplots(6, 8, subplot_kw=dict(xticks=[], yticks=[]))for i, axi in enumerate(ax.flat): axi.imshow(mnist.data[1250 * i].reshape(28, 28), cmap='gray_r')
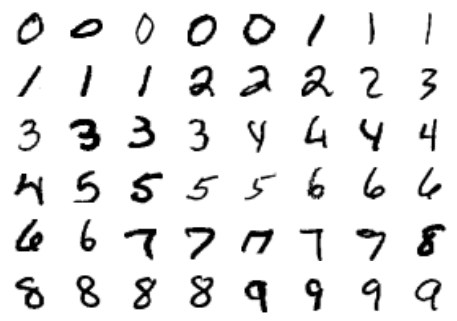
Điều này cho chúng ta một ý tưởng về sự đa dạng của các kiểu viết tay trong tập dữ liệu.
Chúng ta hãy tính toán một projection manifold learning trên dữ liệu.Vì tốc độ, ở đây chúng ta chỉ sử dụng 1/30 dữ liệu, đó là khoảng ~2000 điểm(Vì phương pháp manifold learning không mở rộng tốt, tôi tìm thấy một vài nghìn mẫu là một con số tốt để bắt đầu với việc khám phá nhanh chóng trước khi chuyển sang tính toán đầy đủ):
# use only 1/30 of the data: full dataset takes a long time!data = mnist.data[::30]target = mnist.target[::30]model = Isomap(n_components=2)proj = model.fit_transform(data)plt.scatter(proj[:, 0], proj[:, 1], c=target, cmap=plt.cm.get_cmap('jet', 10))plt.colorbar(ticks=range(10))plt.clim(-0.5, 9.5);
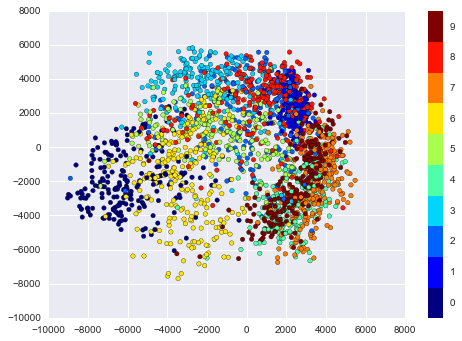
Biểu đồ phân tán kết quả hiển thị một số mối quan hệ giữa các điểm dữ liệu, nhưng hơi đông đúc.Chúng ta có thể có được cái nhìn rõ hơn bằng cách chỉ xem một số đơn lẻ một cách duy nhất:
from sklearn.manifold import Isomap# Choose 1/4 of the "1" digits to projectdata = mnist.data[mnist.target == 1][::4]fig, ax = plt.subplots(figsize=(10, 10))model = Isomap(n_neighbors=5, n_components=2, eigen_solver='dense')plot_components(data, model, images=data.reshape((-1, 28, 28)), ax=ax, thumb_frac=0.05, cmap='gray_r')
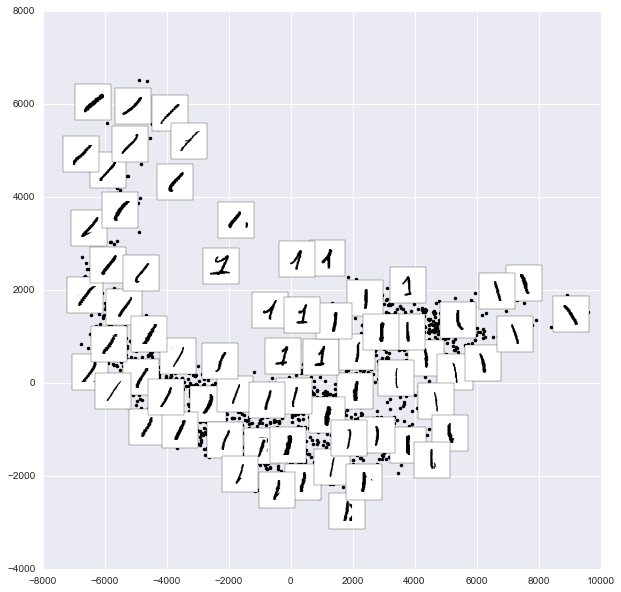
Kết quả cung cấp cho bạn một ý tưởng về sự đa dạng của các dạng số “1” có thể có trong tập dữ liệu.Dữ liệu nằm dọc theo một đường cong rộng trong không gian dự án, có vẻ như theo vết chiều hướng của chữ số.Khi bạn di chuyển lên trên đồ thị, bạn sẽ tìm thấy các số “1” mà có nón và/hoặc đáy, tuy nhiên chúng rất ít trong tập dữ liệu.Dự án cho phép chúng ta xác định các điểm ngoại lệ có vấn đề về dữ liệu: ví dụ như các phần của các chữ số lân cận đã trốn vào các hình ảnh trích xuất.
Bây giờ, điều này tự nó có thể không hữu ích cho việc phân loại chữ số, nhưng nó giúp chúng ta hiểu về dữ liệu và có thể đưa ra ý tưởng về cách tiến xa hơn, chẳng hạn như cách chúng ta có thể muốn tiền xử lý dữ liệu trước khi xây dựng một đường ống phân loại.








