Giới thiệu về phân tích thành phần chính¶
Phân tích thành phần chính là một phương pháp không giám sát nhanh chóng và linh hoạt để giảm chiều dữ liệu, mà chúng ta đã thấy qua trang Giới thiệu Scikit-Learn.Hành vi của nó dễ nhìn thấy nhất thông qua việc xem xét một tập dữ liệu hai chiều.Hãy xem xét 200 điểm dữ liệu sau đây:
rng = np.random.RandomState(1)X = np.dot(rng.rand(2, 2), rng.randn(2, 200)).Tplt.scatter(X[:, 0], X[:, 1])plt.axis('equal');
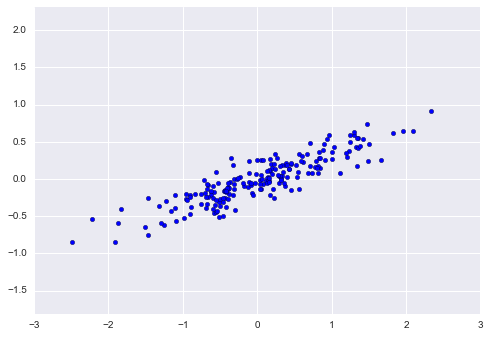
Mắt thường, rõ ràng có một mối quan hệ gần như tuyến tính giữa các biến x và y.Điều này gợi nhớ đến dữ liệu hồi quy tuyến tính mà chúng ta đã khám phá trong In Depth: Linear Regression, nhưng bài toán ở đây có một chút khác biệt: thay vì cố gắng dự đoán giá trị y từ các giá trị x, bài toán học không giám sát cố gắng tìm hiểu về mối quan hệ giữa các giá trị x và y.
Trong phân tích thành phần chính, mối quan hệ này được định lượng bằng cách tìm một danh sách các trục chính trong dữ liệu và sử dụng những trục đó để mô tả tập dữ liệu.Sử dụng bộ ước lượng PCA của Scikit-Learn, chúng ta có thể tính toán như sau:
from sklearn.decomposition import PCApca = PCA(n_components=2)pca.fit(X)
PCA(copy=True, n_components=2, whiten=False)
Phương pháp tính toán học học được một số đại lượng từ dữ liệu, quan trọng nhất là “các thành phần” và “phương sai giải thích”:
print(pca.components_)
[[ 0.94446029 0.32862557] [ 0.32862557 -0.94446029]]
print(pca.explained_variance_)
[ 0.75871884 0.01838551]
Để hiểu ý nghĩa của những con số này, hãy hình dung chúng như các vector trên dữ liệu đầu vào, sử dụng “thành phần” để xác định hướng của vector và “phương sai đã giải thích” để xác định độ dài bình phương của vector:
def draw_vector(v0, v1, ax=None): ax = ax or plt.gca() arrowprops=dict(arrowstyle='->', linewidth=2, shrinkA=0, shrinkB=0) ax.annotate('', v1, v0, arrowprops=arrowprops)# plot dataplt.scatter(X[:, 0], X[:, 1], alpha=0.2)for length, vector in zip(pca.explained_variance_, pca.components_): v = vector * 3 * np.sqrt(length) draw_vector(pca.mean_, pca.mean_ + v)plt.axis('equal');
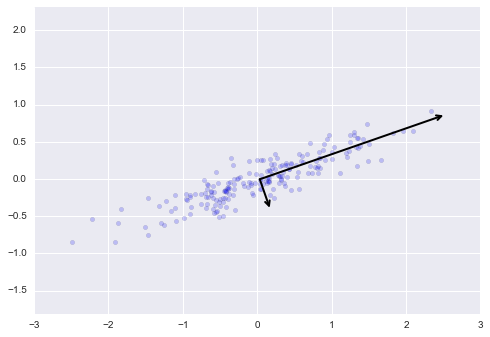
Các vector này đại diện cho các trục chính của dữ liệu, và độ dài của vector là một chỉ số cho thấy mức độ “quan trọng” của trục đó trong việc mô tả phân phối của dữ liệu – cụ thể hơn, nó là một chỉ số của phương sai của dữ liệu khi được chiếu lên trục đó.Chiếu mỗi điểm dữ liệu lên các trục chính đó là các “thành phần chính” của dữ liệu.
Nếu chúng ta vẽ các thành phần chính này cạnh bên dữ liệu gốc, chúng ta sẽ thấy các đồ thị được hiển thị ở đây:
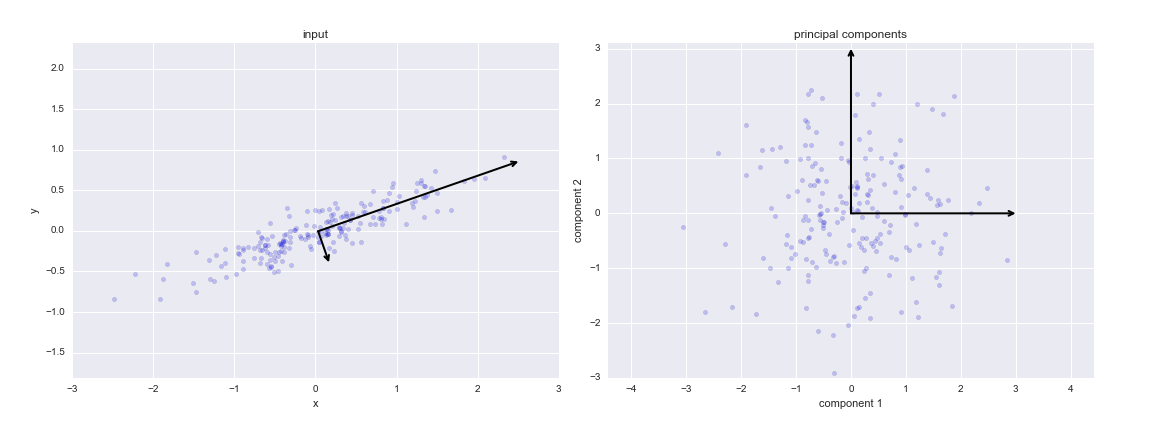
Quá trình chuyển đổi này từ trục dữ liệu sang trục chính là một phép biến đổi tuyến tính, điều này có nghĩa đơn giản là nó được tạo thành từ một phép dịch chuyển, xoay và tỉ lệ đồng nhất.
Mặc dù thuật toán này để tìm các thành phần chính có thể có vẻ chỉ là một sự tò mò toán học, nhưng nó lại có ứng dụng rất rộng trong lĩnh vực học máy và khám phá dữ liệu.
PCA như một phương pháp giảm chiều dữ liệu¶
Sử dụng PCA (Phân tích thành phần chính) để giảm chiều dữ liệu liên quan đến việc làm cho một hoặc nhiều thành phần chính nhỏ nhất bằng không, dẫn đến một phản chiếu chiều thấp hơn của dữ liệu giữ nguyên phương sai dữ liệu tối đa.
Dưới đây là một ví dụ về việc sử dụng PCA như một phép biến đổi giảm chiều:
pca = PCA(n_components=1)pca.fit(X)X_pca = pca.transform(X)print("original shape: ", X.shape)print("transformed shape:", X_pca.shape)
original shape: (200, 2)transformed shape: (200, 1)
Dữ liệu đã được biến đổi đã được giảm xuống một chiều duy nhất.Để hiểu hiệu ứng của việc giảm chiều này, chúng ta có thể thực hiện việc biến đổi nghịch đảo của dữ liệu đã được giảm này và vẽ nó cùng với dữ liệu ban đầu:
X_new = pca.inverse_transform(X_pca)plt.scatter(X[:, 0], X[:, 1], alpha=0.2)plt.scatter(X_new[:, 0], X_new[:, 1], alpha=0.8)plt.axis('equal');
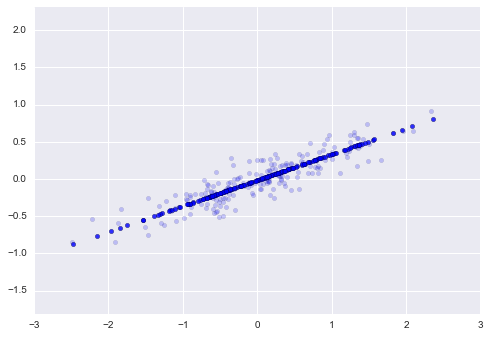
Các điểm sáng là dữ liệu gốc, trong khi các điểm tối là phiên bản đã được chiếu.Điều này làm rõ ý nghĩa của việc giảm số chiều PCA: thông tin trên trục hoặc trục chính không quan trọng nhất được loại bỏ, chỉ còn lại các thành phần của dữ liệu có phương sai cao nhất.Tỷ lệ phương sai đã được loại bỏ (tương ứng với sự lan rộng của các điểm xung quanh đường thẳng trong hình vẽ này) đại khái là một đo lường cho việc “thông tin” bị bỏ đi trong quá trình giảm số chiều này.
Bộ dữ liệu giảm chiều này có thể coi là “đủ tốt” để mã hóa những quan hệ quan trọng nhất giữa các điểm: mặc dù giảm chiều dữ liệu đi 50%, tổng quan quan hệ giữa các điểm dữ liệu vẫn được bảo tồn chủ yếu.
PCA for visualization: Chữ số viết tay¶
Tính hữu ích của việc giảm số chiều có thể không hoàn toàn rõ ràng chỉ trong hai chiều, nhưng trở nên rõ ràng hơn nhiều khi nhìn vào dữ liệu có chiều cao.Để thấy điều này, hãy nhìn nhanh vào ứng dụng PCA vào dữ liệu chữ số mà chúng ta đã thấy trong Sâu hơn: Cây quyết định và Rừng ngẫu nhiên.
Chúng ta bắt đầu bằng việc tải dữ liệu:
from sklearn.datasets import load_digitsdigits = load_digits()digits.data.shape
(1797, 64)
Nhớ rằng dữ liệu gồm các hình ảnh pixel 8×8, có nghĩa là chúng có 64 chiều.Để hiểu thêm về mối quan hệ giữa những điểm này, chúng ta có thể sử dụng PCA để chiếu chúng xuống một số chiều quản lý được hơn, ví dụ như hai:
pca = PCA(2) # project from 64 to 2 dimensionsprojected = pca.fit_transform(digits.data)print(digits.data.shape)print(projected.shape)
(1797, 64)(1797, 2)
Chúng ta hiện đã có thể vẽ biểu đồ hai thành phần chính đầu tiên của mỗi điểm để tìm hiểu về dữ liệu:
plt.scatter(projected[:, 0], projected[:, 1], c=digits.target, edgecolor='none', alpha=0.5, cmap=plt.cm.get_cmap('spectral', 10))plt.xlabel('component 1')plt.ylabel('component 2')plt.colorbar();
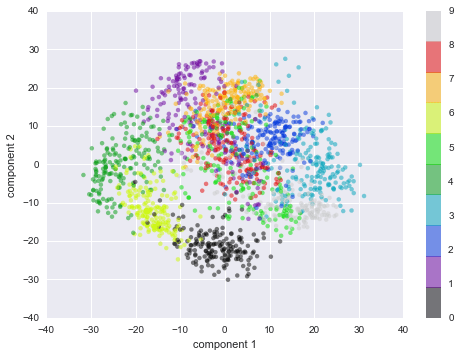
Nhớ lại ý nghĩa của các thành phần này: dữ liệu đầy đủ là một điểm ở không gian 64 chiều, và các điểm này là phép chiếu của mỗi điểm dữ liệu theo hướng có phương sai lớn nhất.Cơ bản, chúng ta đã tìm ra công thức kéo dài và xoay tối ưu trong không gian 64 chiều cho phép chúng ta nhìn thấy cấu trúc của các số trong hai chiều, và đã thực hiện điều này theo cách không giám sát — nghĩa là không cần tham chiếu đến nhãn.
Ý nghĩa của các thành phần là gì?¶
Chúng ta có thể đi xa hơn nữa ở đây, và bắt đầu hỏi những gì ý nghĩa của các chiều giảm đi. Ý nghĩa này có thể được hiểu trong các kết hợp của các vector cơ sở. Ví dụ, mỗi hình ảnh trong bộ dữ liệu huấn luyện được xác định bởi một tập hợp giá trị điểm ảnh 64, mà chúng ta sẽ gọi là vector $x$:
$$x = [x_1, x_2, x_3 \cdots x_{64}]$$
Một cách chúng ta có thể suy nghĩ về điều này là theo cơ sở đơn vị pixel.Đó là, để xây dựng hình ảnh, chúng ta nhân từng phần tử của vector với pixel mà nó mô tả và sau đó cộng kết quả lại với nhau để xây dựng hình ảnh:
$${\rm image}(x) = x_1 \cdot{\rm (pixel~1)} + x_2 \cdot{\rm (pixel~2)} + x_3 \cdot{\rm (pixel~3)} \cdots x_{64} \cdot{\rm (pixel~64)}$$
Một cách chúng ta có thể tưởng tượng để giảm số chiều của dữ liệu này là đưa tất cả các vector cơ sở này về số không, chỉ giữ lại một số vector cơ sở.

Hàng trên của các bảng trình bày các pixel riêng lẻ, và hàng dưới trình bày sự đóng góp tích lũy của các pixel này vào việc xây dựng hình ảnh.Chỉ sử dụng tám trong số các thành phần cơ sở của pixel, chúng ta chỉ có thể xây dựng một phần nhỏ của hình ảnh 64 pixel.Nếu chúng ta tiếp tục chuỗi này và sử dụng tất cả 64 pixel, chúng ta sẽ khôi phục lại hình ảnh ban đầu.
Tuy nhiên, biểu diễn theo từng pixel không phải là lựa chọn duy nhất. Chúng ta cũng có thể sử dụng các hàm cơ sở khác, mà mỗi hàm chứa một đóng góp được xác định trước từ mỗi pixel và viết một cái gì đó như thế này
$$hình\_ảnh(x) = trung\_bình + x_1 \cdot{\rm (cơ\_sở~1)} + x_2 \cdot{\rm (cơ\_sở~2)} + x_3 \cdot{\rm (cơ\_sở~3)} \cdots$$
PCA có thể được coi là quá trình chọn các hàm cơ sở tối ưu, sao cho chỉ cần cộng lại một số ít trong số chúng là đủ để xây dựng lại được hầu hết các phần tử trong bộ dữ liệu.Các thành phần chính, đóng vai trò là biểu diễn chiều thấp của dữ liệu của chúng ta, đơn giản chỉ là các hệ số nhân với mỗi phần tử trong chuỗi này.Hình này cho thấy một hình dung tương tự về việc xây dựng lại chữ số này bằng cách sử dụng trung bình cộng cùng tám hàm cơ sở PCA đầu tiên:

Khác với cơ sở pixel, cơ sở PCA cho phép chúng ta khôi phục những đặc điểm nổi bật của ảnh đầu vào chỉ với một trung bình cộng cộng tám thành phần!Lượng mỗi pixel trong mỗi thành phần là hậu quả của hướng của vector trong ví dụ hai chiều của chúng ta.Đây là cách mà PCA cung cấp một biểu diễn chiều thấp của dữ liệu: nó khám phá một tập hàm cơ sở hiệu quả hơn so với cơ sở pixel mặc định của dữ liệu đầu vào.
Chọn số lượng thành phần
Một phần quan trọng trong việc sử dụng PCA trong thực tế là khả năng ước lượng số lượng thành phần cần thiết để mô tả dữ liệu.Điều này có thể được xác định bằng cách nhìn vào tỷ lệ giải thích phương sai cộng dồn theo số lượng thành phần:
pca = PCA().fit(digits.data)plt.plot(np.cumsum(pca.explained_variance_ratio_))plt.xlabel('number of components')plt.ylabel('cumulative explained variance');
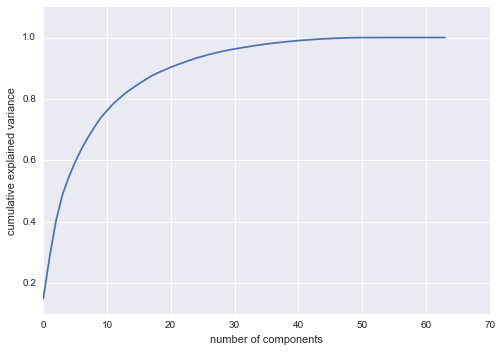
Đường cong này có số học hóa biểu diễn lượng phương sai 64 chiều tổng quát nằm trong $N$ thành phần đầu tiên.Ví dụ, ta thấy rằng với số, 10 thành phần đầu tiên chứa khoảng 75% phương sai, trong khi bạn cần khoảng 50 thành phần để mô tả gần như 100% phương sai.
Ở đây, chúng ta nhận thấy rằng phép chiếu hai chiều của chúng ta mất mát rất nhiều thông tin (được đo bằng phương sai giải thích) và chúng ta sẽ cần khoảng 20 thành phần để giữ lại 90% phương sai. Nhìn vào biểu đồ này của một bộ dữ liệu có chiều cao có thể giúp bạn hiểu mức độ trùng lặp có mặt trong nhiều quan sát.
PCA làm bộ lọc nhiễu¶
PCA cũng có thể được sử dụng như một phương pháp lọc dữ liệu nhiễu.
Hãy xem xét xem điều này trông như thế nào với dữ liệu số.
def plot_digits(data): fig, axes = plt.subplots(4, 10, figsize=(10, 4), subplot_kw={'xticks':[], 'yticks':[]}, gridspec_kw=dict(hspace=0.1, wspace=0.1)) for i, ax in enumerate(axes.flat): ax.imshow(data[i].reshape(8, 8), cmap='binary', interpolation='nearest', clim=(0, 16))plot_digits(digits.data)
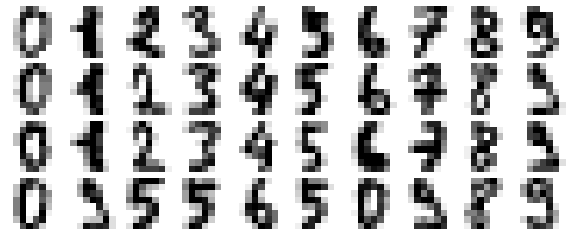
Bây giờ chúng ta hãy thêm một số nhiễu ngẫu nhiên để tạo ra một tập dữ liệu ồn ào, và vẽ lại nó:
np.random.seed(42)noisy = np.random.normal(digits.data, 4)plot_digits(noisy)
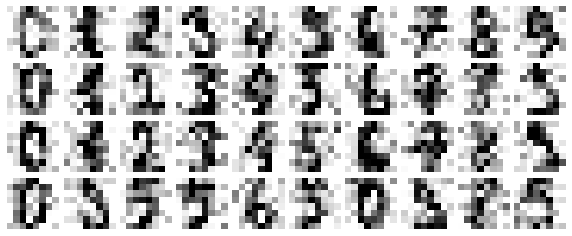
Thông qua mắt thường, có thể thấy rõ rằng hình ảnh có nhiễu và chứa các pixel giả. Hãy huấn luyện một PCA trên dữ liệu nhiễu, yêu cầu rằng phép chiếu này giữ lại 50% phương sai:
pca = PCA(0.50).fit(noisy)pca.n_components_
12
Ở đây, 50% của sự biến đổi tương ứng với 12 thành phần chính.Bây giờ chúng ta tính toán các thành phần này và sau đó sử dụng nghịch đảo của quá trình biến đổi để tái tạo các chữ số đã được lọc:
components = pca.transform(noisy)filtered = pca.inverse_transform(components)plot_digits(filtered)
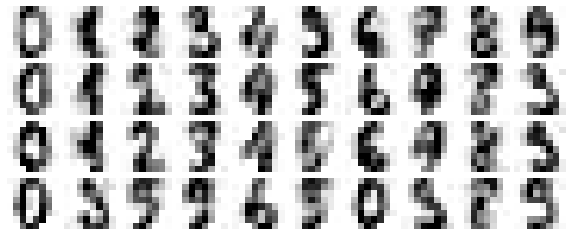
Thuộc tính bảo tồn tín hiệu/lọc nhiễu này khiến PCA trở thành một quá trình lựa chọn đặc trưng rất hữu ích – ví dụ, thay vì huấn luyện một bộ phân loại trên dữ liệu có kích thước rất cao, bạn có thể huấn luyện bộ phân loại trên biểu diễn có số chiều thấp hơn, mà tự động sẽ loại bỏ nhiễu ngẫu nhiên trong đầu vào.
Ví dụ: Eigenfaces¶
Trước đó chúng ta đã khám phá một ví dụ về việc sử dụng PCA projection như một bộ chọn đặc trưng cho nhận dạng khuôn mặt với máy vector hỗ trợ (xem Sâu Hơn: Máy Vector Hỗ Trợ).Ở đây chúng ta sẽ nhìn lại và khám phá thêm một chút về những gì đã được thực hiện.Hãy nhớ rằng chúng ta đã sử dụng bộ dữ liệu Labeled Faces in the Wild được cung cấp thông qua Scikit-Learn:
from sklearn.datasets import fetch_lfw_peoplefaces = fetch_lfw_people(min_faces_per_person=60)print(faces.target_names)print(faces.images.shape)
['Ariel Sharon' 'Colin Powell' 'Donald Rumsfeld' 'George W Bush' 'Gerhard Schroeder' 'Hugo Chavez' 'Junichiro Koizumi' 'Tony Blair'](1348, 62, 47)
Hãy cùng xem các trục chính mà chúng ta có trong tập dữ liệu này.Bởi vì đây là một tập dữ liệu lớn, chúng ta sẽ sử dụng RandomizedPCA – nó chứa một phương pháp ngẫu nhiên để xấp xỉ $N$ thành phần chính đầu tiên một cách nhanh chóng hơn so với phương pháp truyền thống của PCA, và do đó rất hữu ích cho dữ liệu có số chiều cao (ở đây gần 3.000 chiều).Chúng ta sẽ xem xét 150 thành phần đầu tiên:
from sklearn.decomposition import RandomizedPCApca = RandomizedPCA(150)pca.fit(faces.data)
RandomizedPCA(copy=True, iterated_power=3, n_components=150, random_state=None, whiten=False)
Trong trường hợp này, có thể thú vị để hình dung các hình ảnh liên quan đến một số thành phần chính đầu tiên (những thành phần này kỹ thuật được gọi là “eigenvectors,” vì vậy những loại hình ảnh này thường được gọi là “eigenfaces”).
fig, axes = plt.subplots(3, 8, figsize=(9, 4), subplot_kw={'xticks':[], 'yticks':[]}, gridspec_kw=dict(hspace=0.1, wspace=0.1))for i, ax in enumerate(axes.flat): ax.imshow(pca.components_[i].reshape(62, 47), cmap='bone')

Kết quả là rất thú vị và cho chúng ta cái nhìn sâu sắc vào cách các hình ảnh thay đổi: ví dụ, một số eigenfaces đầu tiên (ở góc trên bên trái) dường như liên quan đến góc chiếu sáng trên khuôn mặt, và các vector chính sau đó dường như chọn lọc ra các đặc điểm cụ thể như mắt, mũi và môi.Hãy xem tổng tích lũy của phương sai của các thành phần này để xem mức độ thông tin dữ liệu mà phép chiếu đang bảo tồn:
plt.plot(np.cumsum(pca.explained_variance_ratio_))plt.xlabel('number of components')plt.ylabel('cumulative explained variance');
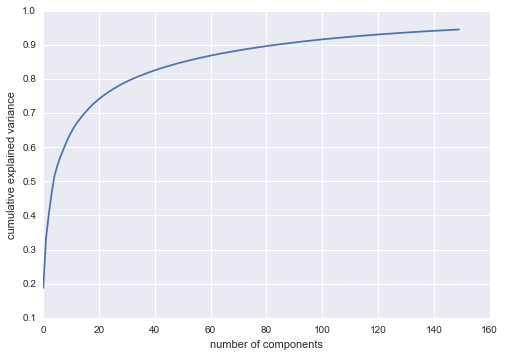
Chúng ta nhìn thấy rằng 150 thành phần này chiếm hơn 90% phương sai.Điều đó sẽ dẫn chúng ta tin rằng sử dụng 150 thành phần này, chúng ta sẽ khôi phục lại phần lớn các đặc điểm cần thiết của dữ liệu.Để làm cho điều này cụ thể hơn, chúng ta có thể so sánh các hình ảnh đầu vào với các hình ảnh được tái tạo từ 150 thành phần này:
# Compute the components and projected facespca = RandomizedPCA(150).fit(faces.data)components = pca.transform(faces.data)projected = pca.inverse_transform(components)
# Plot the resultsfig, ax = plt.subplots(2, 10, figsize=(10, 2.5), subplot_kw={'xticks':[], 'yticks':[]}, gridspec_kw=dict(hspace=0.1, wspace=0.1))for i in range(10): ax[0, i].imshow(faces.data[i].reshape(62, 47), cmap='binary_r') ax[1, i].imshow(projected[i].reshape(62, 47), cmap='binary_r') ax[0, 0].set_ylabel('full-dim\ninput')ax[1, 0].set_ylabel('150-dim\nreconstruction');

Dòng đầu tiên ở đây hiển thị các hình ảnh đầu vào, trong khi dòng dưới hiển thị việc tái tạo hình ảnh từ chỉ 150 trong số khoảng 3.000 đặc trưng ban đầu.
Tóm tắt phân tích thành phần chính
Trong phần này, chúng ta đã thảo luận về việc sử dụng phân tích thành phần chính để giảm số chiều dữ liệu, để tạo ra hình ảnh của dữ liệu có số chiều cao, để lọc nhiễu và để chọn đặc trưng trong dữ liệu có số chiều cao.Do tính linh hoạt và khả năng giải thích của PCA, nó đã được chứng minh là hiệu quả trong nhiều ngữ cảnh và lĩnh vực khác nhau.Cho bất kỳ bộ dữ liệu có số chiều cao nào, tôi thường bắt đầu bằng PCA để hiển thị mối quan hệ giữa các điểm (như chúng ta đã làm với các chữ số), để hiểu phương sai chính trong dữ liệu (như chúng ta đã làm với khuôn mặt chính riêng), và để hiểu số chiều nội tại (bằng cách vẽ biểu đồ tỷ lệ phương sai được giải thích).Chắc chắn PCA không hữu ích cho mọi bộ dữ liệu có số chiều cao, nhưng nó cung cấp một con đường trực tiếp và hiệu quả để hiểu sâu về dữ liệu có số chiều cao.
Điểm yếu chính của PCA là nó dễ bị ảnh hưởng bởi các giá trị ngoại lệ trong dữ liệu.Vì lý do này, nhiều biến thể mạnh mẽ của PCA đã được phát triển, trong đó có nhiều biến thể hoạt động để lần lượt loại bỏ các điểm dữ liệu mà các thành phần ban đầu không mô tả tốt.Scikit-Learn bao gồm một số biến thể thú vị về PCA, bao gồm RandomizedPCA và SparsePCA, cả hai cũng nằm trong phụ mô-đun sklearn.decomposition.RandomizedPCA, mà chúng ta đã thấy trước đó, sử dụng phương pháp không xác định để xấp xỉ nhanh các thành phần chính đầu tiên trong dữ liệu có số chiều rất cao, trong khi SparsePCA giới thiệu một thuật ngữ chính quy hóa (xem Sâu trong: Hồi quy tuyến tính) để bắt buộc phần hiện thân của các thành phần.
Trong các phần tiếp theo, chúng ta sẽ xem xét các phương pháp học không giám sát khác mà xây dựng dựa trên một số ý tưởng của PCA.









