Các Lổi Cơ Bản¶
Một lỗi cơ bản có thể được tạo ra bằng một lệnh gọi hàm Matplotlib duy nhất:
%matplotlib inlineimport matplotlib.pyplot as pltplt.style.use('seaborn-whitegrid')import numpy as np
x = np.linspace(0, 10, 50)dy = 0.8y = np.sin(x) + dy * np.random.randn(50)plt.errorbar(x, y, yerr=dy, fmt='.k');
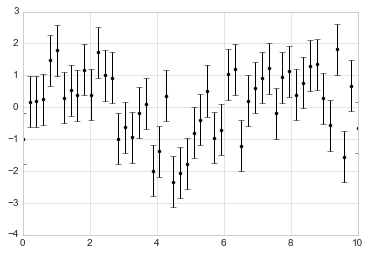
Ở đây, fmt là một mã định dạng điều khiển hiển thị các dòng và điểm, và có cú pháp giống với các cú pháp viết tắt được sử dụng trong plt.plot, được trình bày trong Biểu đồ Đường đơn giản và Biểu đồ Phân tán đơn giản.
Ngoài những tùy chọn cơ bản này, hàm errorbar còn có nhiều tùy chọn khác để điều chỉnh kết quả một cách tinh vi.Sử dụng những tùy chọn bổ sung này, bạn có thể dễ dàng tùy chỉnh vẻ đẹp của biểu đồ errorbar của mình.Thường thấy hữu ích, đặc biệt trong biểu đồ đông đúc, khiến các thanh lỗi nhạt hơn so với điểm mà chúng biểu thị:
plt.errorbar(x, y, yerr=dy, fmt='o', color='black', ecolor='lightgray', elinewidth=3, capsize=0);

Ngoài những tùy chọn này, bạn cũng có thể chỉ định thanh lỗi theo chiều ngang (xerr), thanh lỗi một mặt và nhiều biến thể khác.Để biết thêm thông tin về các tùy chọn có sẵn, hãy tham khảo docstring của plt.errorbar.
Lỗi liên tục¶
Trong một số tình huống, việc hiển thị thanh lỗi trên các đại lượng liên tục là mong muốn.Mặc dù Matplotlib không có một công cụ tiện ích tích hợp sẵn cho loại ứng dụng này, nhưng việc kết hợp các nguyên tố như plt.plot và plt.fill_between để đạt được kết quả hữu ích là khá dễ dàng.
Ở đây chúng ta sẽ thực hiện một quá trình hồi quy Gaussian cơ bản, sử dụng API Scikit-Learn (xem Giới thiệu Scikit-Learn để biết thêm chi tiết).Đây là một phương pháp để phù hợp một hàm phi tham số linh hoạt rất đa dạng với dữ liệu có thước đo liên tục về sự không chắc chắn.Ở đây chúng tôi sẽ không đi sâu vào chi tiết của quá trình hồi quy Gaussian mà thay vào đó sẽ tập trung vào cách bạn có thể trực quan hóa đo lường lỗi liên tục như thế này:
from sklearn.gaussian_process import GaussianProcess# define the model and draw some datamodel = lambda x: x * np.sin(x)xdata = np.array([1, 3, 5, 6, 8])ydata = model(xdata)# Compute the Gaussian process fitgp = GaussianProcess(corr='cubic', theta0=1e-2, thetaL=1e-4, thetaU=1E-1, random_start=100)gp.fit(xdata[:, np.newaxis], ydata)xfit = np.linspace(0, 10, 1000)yfit, MSE = gp.predict(xfit[:, np.newaxis], eval_MSE=True)dyfit = 2 * np.sqrt(MSE) # 2*sigma ~ 95% confidence region
Bây giờ chúng ta có xfit, yfit và dyfit, các biến này mẫu lấy các giá trị liên tục cho dữ liệu của chúng ta.Chúng ta có thể truyền chúng vào hàm plt.errorbar như đã nêu ở trên, nhưng chúng ta thực sự không muốn vẽ 1,000 điểm với 1,000 cây đo lỗi.Thay vào đó, chúng ta có thể sử dụng hàm plt.fill_between với một màu nhạt để hình dung cây đo lỗi liên tục này:
# Visualize the resultplt.plot(xdata, ydata, 'or')plt.plot(xfit, yfit, '-', color='gray')plt.fill_between(xfit, yfit - dyfit, yfit + dyfit, color='gray', alpha=0.2)plt.xlim(0, 10);
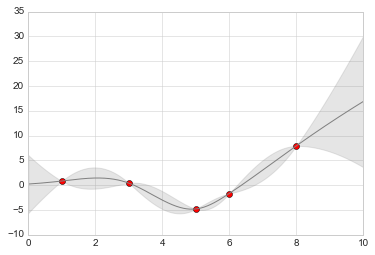
Lưu ý những gì chúng ta đã làm ở đây với hàm fill_between: chúng ta truyền một giá trị x, sau đó là giới hạn y thấp, sau đó là giới hạn y cao và kết quả là khu vực giữa các khu vực này được điền.
Kết quả cho một hình vẽ rất trực quan về những gì thuật toán hồi quy quy trình Gaussian đang thực hiện: trong các khu vực gần một điểm dữ liệu đã đo, mô hình được ràng buộc mạnh mẽ và điều này được phản ánh trong các lỗi mô hình nhỏ.Trong các khu vực xa khỏi một điểm dữ liệu đã đo, mô hình không bị ràng buộc mạnh mẽ, và các lỗi mô hình tăng lên.
Để biết thêm thông tin về các tùy chọn có sẵn trong plt.fill_between() (và hàm plt.fill() có liên quan), xem docstring của hàm hoặc tài liệu của Matplotlib.
Cuối cùng, nếu điều này có vẻ hơi cấp thấp đối với khẩu vị của bạn, hãy tham khảo Visualization With Seaborn, nơi chúng tôi thảo luận về gói Seaborn, có một API được tối ưu hóa hơn để trực quan hóa loại lỗi liên tục này.









