Phân loại Bayesian¶
Bộ phân loại Naive Bayes được xây dựng trên phương pháp phân loại Bayes.Các bước này dựa trên định lý của Bayes, đây là một phương trình mô tả mối quan hệ của xác suất điều kiện của các đại lượng thống kê.Trong phân loại Bayes, chúng ta quan tâm đến việc tìm xác suất của một nhãn đã biết một số đặc trưng quan sát được, điều này có thể được viết dưới dạng $P(L~|~{\rm features})$.Định lý của Bayes cho chúng ta biết cách biểu diễn điều này dưới dạng các đại lượng chúng ta có thể tính toán trực tiếp:
$$P(L~|~{\rm features}) = \frac{P({\rm features}~|~L)P(L)}{P({\rm features})}$$
Nếu chúng ta đang cố gắng lựa chọn giữa hai nhãn – hãy gọi là $L_1$ và $L_2$ – thì một cách để đưa ra quyết định là tính tỷ lệ giữa xác suất hậu nghiệm cho mỗi nhãn:
NoneMọi thứ chúng ta cần lúc này chỉ là một mô hình để tính toán $P({\rm features}~|~L_i)$ cho mỗi nhãn.Một mô hình như vậy được gọi là một mô hình sinh vì nó chỉ định quá trình ngẫu nhiên giả định tạo ra dữ liệu.Đặc tả mô hình sinh này cho mỗi nhãn là một phần chính của việc huấn luyện của một bộ phân loại Bayesian như vậy.Phiên bản tổng quát của bước huấn luyện như vậy là một nhiệm vụ rất khó khăn, nhưng chúng ta có thể làm cho nó đơn giản hơn thông qua việc sử dụng một số giả định đơn giản về hình thức của mô hình này.
Đây là nơi “ngây thơ” trong “naive Bayes”: nếu chúng ta đặt ra những giả định cực kỳ ngây thơ về mô hình sinh ra cho mỗi nhãn, chúng ta có thể tìm một xấp xỉ sơ bộ của mô hình sinh ra cho mỗi lớp, sau đó tiếp tục với phân loại Bayesian.Các loại bộ phân loại naive Bayes khác nhau đòi hỏi những giả định ngây thơ khác nhau về dữ liệu, và chúng ta sẽ xem xét một số loại này trong các phần tiếp theo.
Đầu tiên chúng ta bắt đầu với các import chuẩn:
%matplotlib inlineimport numpy as npimport matplotlib.pyplot as pltimport seaborn as sns; sns.set()
Gaussian Naive Bayes¶
Có thể nhận thấy, một trong những bộ phân lớp naive Bayes đơn giản nhất để hiểu là naive Bayes Gaussian.Trong bộ phân lớp này, giả định là dữ liệu từ mỗi nhãn được rút từ một phân phối Gaussian đơn giản.Hãy tưởng tượng bạn có dữ liệu sau:
from sklearn.datasets import make_blobsX, y = make_blobs(100, 2, centers=2, random_state=2, cluster_std=1.5)plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='RdBu');
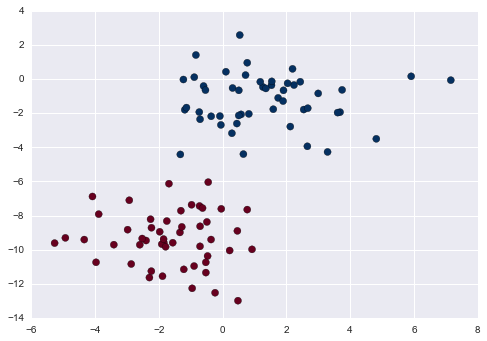
Một cách cực kỳ nhanh chóng để tạo ra một mô hình đơn giản là giả định rằng dữ liệu được mô tả bằng phân phối Gaussian với không có sự tương quan giữa các chiều.
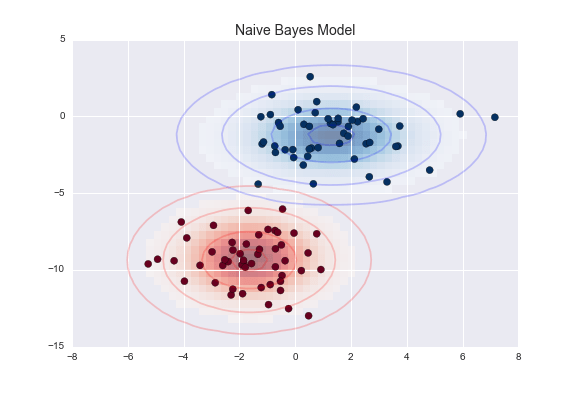
Các dấu elip ở đây đại diện cho mô hình sinh ra Gaussian cho mỗi nhãn, với xác suất lớn hơn hướng tới phần trung tâm của các dấu elip.Với mô hình sinh ra này đối với mỗi lớp, chúng ta có công thức đơn giản để tính xác suất $P({\rm features}~|~L_1)$ cho bất kỳ điểm dữ liệu nào, và do đó chúng ta có thể nhanh chóng tính toán tỷ lệ hậu nghiệm và xác định nhãn nào là có xác suất cao nhất cho một điểm dữ liệu cụ thể.
Thủ tục này được triển khai trong bộ ước lượng sklearn.naive_bayes.GaussianNB của Scikit-Learn:
from sklearn.naive_bayes import GaussianNBmodel = GaussianNB()model.fit(X, y);
Bây giờ hãy tạo ra một số dữ liệu mới và dự đoán nhãn:
rng = np.random.RandomState(0)Xnew = [-6, -14] + [14, 18] * rng.rand(2000, 2)ynew = model.predict(Xnew)
Bây giờ chúng ta có thể vẽ biểu đồ dữ liệu mới này để có được một ý tưởng về vị trí của ranh giới quyết định:
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='RdBu')lim = plt.axis()plt.scatter(Xnew[:, 0], Xnew[:, 1], c=ynew, s=20, cmap='RdBu', alpha=0.1)plt.axis(lim);
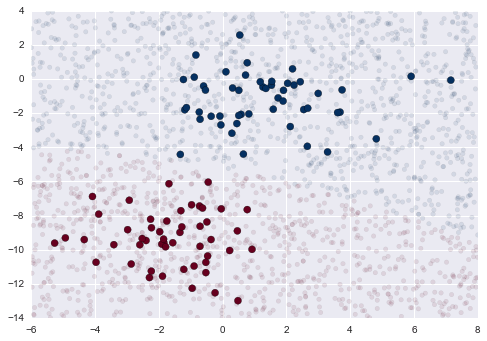
Chúng ta thấy một ranh giới hơi cong trong các phân loại – nói chung, ranh giới trong Gaussian naive Bayes là hình bậc hai.
Một mảnh tuyệt vời của hình thức Bayesian này là nó tự nhiên cho phép phân loại xác suất, mà chúng ta có thể tính bằng cách sử dụng phương thức predict_proba:
yprob = model.predict_proba(Xnew)yprob[-8:].round(2)
array([[ 0.89, 0.11], [ 1. , 0. ], [ 1. , 0. ], [ 1. , 0. ], [ 1. , 0. ], [ 1. , 0. ], [ 0. , 1. ], [ 0.15, 0.85]])
Các cột cho các xác suất hậu nghiệm của nhãn đầu tiên và nhãn thứ hai, tương ứng.Nếu bạn đang tìm kiếm ước lượng không chắc chắn trong phân loại của bạn, các phương pháp Bayesian như này có thể là một phương pháp hữu ích.
Tất nhiên, phân loại cuối cùng chỉ tốt như các giả định mô hình dẫn đến nó, đó là lý do tại sao Gaussian naive Bayes thường không cho kết quả tốt.Tuy nhiên, trong nhiều trường hợp – đặc biệt là khi số lượng đặc trưng trở nên lớn – giả định này không gây thiệt hại đủ để ngăn cản Gaussian naive Bayes trở thành một phương pháp hữu ích.
Multinomial Naive Bayes¶
Giả thuyết Gaussian vừa được mô tả không phải là giả thuyết đơn giản duy nhất có thể được sử dụng để chỉ định phân phối sinh ngẫu nhiên cho mỗi nhãn.Một ví dụ hữu ích khác là naive Bayes đa biến, trong đó giả định các đặc trưng được sinh ra từ một phân phối multinomial đơn giản.Phân phối multinomial mô tả xác suất của việc quan sát các giá trị trong một số loại, và do đó naive Bayes đa biến là phù hợp nhất cho các đặc trưng biểu thị số lượng hoặc tỷ lệ đếm.
Ý tưởng vẫn giống như trước, chỉ khác là thay vì mô hình hóa phân phối dữ liệu bằng phân phối Gaussian tốt nhất, chúng ta mô hình phân phối dữ liệu bằng phân phối đa biến tốt nhất.
Ví dụ: Phân loại văn bản¶
Một nơi mà multinomial naive Bayes thường được sử dụng là trong phân loại văn bản, trong đó các đặc trưng liên quan đến số lượng từ hoặc tần suất trong các tài liệu cần phân loại.Chúng tôi đã thảo luận về việc trích xuất các đặc trưng như vậy từ văn bản trong Feature Engineering; ở đây chúng tôi sẽ sử dụng các đặc trưng đếm từ hiếm từ bộ dữ liệu 20 Newsgroups để cho thấy cách chúng ta có thể phân loại các tài liệu ngắn này vào các danh mục.
Hãy tải dữ liệu và xem tên của mục tiêu:
from sklearn.datasets import fetch_20newsgroupsdata = fetch_20newsgroups()data.target_names
['alt.atheism', 'comp.graphics', 'comp.os.ms-windows.misc', 'comp.sys.ibm.pc.hardware', 'comp.sys.mac.hardware', 'comp.windows.x', 'misc.forsale', 'rec.autos', 'rec.motorcycles', 'rec.sport.baseball', 'rec.sport.hockey', 'sci.crypt', 'sci.electronics', 'sci.med', 'sci.space', 'soc.religion.christian', 'talk.politics.guns', 'talk.politics.mideast', 'talk.politics.misc', 'talk.religion.misc']
Đơn giản ở đây, chúng ta sẽ chỉ chọn một số danh mục này và tải xuống tập huấn luyện và tập kiểm tra:
categories = ['talk.religion.misc', 'soc.religion.christian', 'sci.space', 'comp.graphics']train = fetch_20newsgroups(subset='train', categories=categories)test = fetch_20newsgroups(subset='test', categories=categories)
Đây là một mục đại diện từ dữ liệu:
print(train.data[5])
From: dmcgee@uluhe.soest.hawaii.edu (Don McGee)Subject: Federal HearingOriginator: dmcgee@uluheOrganization: School of Ocean and Earth Science and TechnologyDistribution: usaLines: 10Fact or rumor....? Madalyn Murray O'Hare an atheist who eliminated theuse of the bible reading and prayer in public schools 15 years ago is nowgoing to appear before the FCC with a petition to stop the reading of theGospel on the airways of America. And she is also campaigning to removeChristmas programs, songs, etc from the public schools. If it is truethen mail to Federal Communications Commission 1919 H Street Washington DC20054 expressing your opposition to her request. Reference Petition number2493.
Để sử dụng dữ liệu này cho việc học máy, chúng ta cần chuyển đổi nội dung của mỗi chuỗi thành một vectơ số.
from sklearn.feature_extraction.text import TfidfVectorizerfrom sklearn.naive_bayes import MultinomialNBfrom sklearn.pipeline import make_pipelinemodel = make_pipeline(TfidfVectorizer(), MultinomialNB())
Với đường ống này, chúng ta có thể áp dụng mô hình vào dữ liệu huấn luyện và dự đoán nhãn cho dữ liệu kiểm tra:
model.fit(train.data, train.target)labels = model.predict(test.data)
Bây giờ khi chúng ta đã dự đoán được các nhãn cho dữ liệu kiểm tra, chúng ta có thể đánh giá chúng để tìm hiểu về hiệu suất của bộ dự đoán.Ví dụ, đây là ma trận nhầm lẫn giữa các nhãn thực tế và nhãn dự đoán cho dữ liệu kiểm tra:
from sklearn.metrics import confusion_matrixmat = confusion_matrix(test.target, labels)sns.heatmap(mat.T, square=True, annot=True, fmt='d', cbar=False, xticklabels=train.target_names, yticklabels=train.target_names)plt.xlabel('true label')plt.ylabel('predicted label');
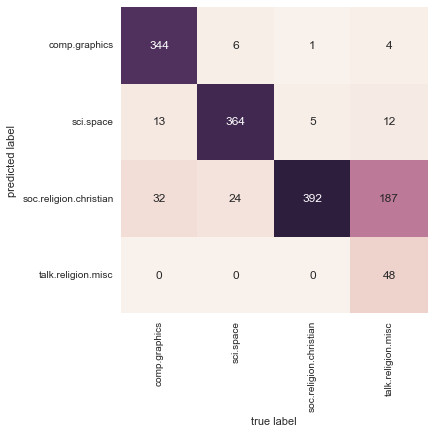
Rõ ràng, ngay cả bộ phân loại rất đơn giản này cũng có thể phân biệt thành công giữa lời nói về không gian và lời nói về máy tính, nhưng nó bị lẫn lộn giữa lời nói về tôn giáo và lời nói về Thiên chúa giáo.Điều này có lẽ là một lĩnh vực nhầm lẫn dễ hiểu!
Điều thú vị ở đây là chúng ta có công cụ để xác định danh mục cho bất kỳ chuỗi nào, sử dụng phương thức predict() của pipeline này.Dưới đây là một hàm tiện ích nhanh sẽ trả về dự đoán cho một chuỗi duy nhất:
def predict_category(s, train=train, model=model): pred = model.predict([s]) return train.target_names[pred[0]]
Hãy thử nghiệm nó:
predict_category('sending a payload to the ISS')
'sci.space'
predict_category('discussing islam vs atheism')
'soc.religion.christian'
predict_category('determining the screen resolution')
'comp.graphics'
Hãy nhớ rằng điều này không phức tạp hơn là một mô hình xác suất đơn giản cho tần suất (được tính toán theo trọng số) của mỗi từ trong chuỗi; tuy nhiên, kết quả là ấn tượng. Ngay cả một thuật toán rất ngây thơ, khi được sử dụng cẩn thận và được huấn luyện trên một tập dữ liệu nhiều chiều lớn, có thể gây ấn tượng mạnh.
Khi nào nên sử dụng Naive Bayes¶
Vì lý thuyết xác suất Bayes ngây thơ đã đưa ra nhiều giả định chặt chẽ về dữ liệu, nên chúng thường không hoạt động hiệu quả bằng một mô hình phức tạp hơn.Tuy nhiên, chúng có một số ưu điểm:
- Chúng rất nhanh cho cả quá trình huấn luyện và dự đoán
- Chúng cung cấp dự đoán xác suất một cách rõ ràng
- Chúng thường rất dễ hiểu
- Chúng có rất ít (nếu có) tham số có thể điều chỉnh
Các ưu điểm này có nghĩa là một bộ phân loại Bayesian ngây thơ thường là lựa chọn tốt như một phân loại dự đoán cơ bản ban đầu.Nếu nó hoạt động đáng mong đợi, thì xin chúc mừng: bạn đã có một bộ phân loại nhanh, dễ hiểu cho vấn đề của bạn.Nếu nó không hoạt động tốt, thì bạn có thể bắt đầu khám phá các mô hình phức tạp hơn, với một số kiến thức cơ bản về mức độ hoạt động của chúng.
Các bộ phân loại Naive Bayes thường hoạt động đặc biệt tốt trong một trong những tình huống sau:
- Khi những giả thiết ngây thơ thật sự phù hợp với dữ liệu (rất hiếm gặp trong thực tế)
- Đối với các category được phân chia rất rõ ràng, khi độ phức tạp của mô hình không quan trọng
- Đối với dữ liệu có số chiều rất cao, khi độ phức tạp của mô hình không quan trọng
Nhìn từ hai điểm cuối cùng dường như khác biệt nhưng thực tế chúng có liên quan: khi kích thước của một tập dữ liệu tăng lên, khả năng hai điểm bất kỳ được tìm thấy gần nhau (tức là chúng phải gần gũi trên tất cả các chiều để gần nhau nói chung) là rất thấp.Điều này có nghĩa là các cụm trong các không gian có số chiều cao thường được phân tách xa hơn, trung bình, so với các cụm trong các không gian có số chiều thấp, miễn là các chiều mới thật sự cung cấp thông tin mới.Vì lý do này, các bộ phân loại đơn giản như naive Bayes thường hoạt động cũng như hoặc tốt hơn các bộ phân loại phức tạp hơn khi số chiều tăng lên: một khi bạn có đủ dữ liệu, thậm chí một mô hình đơn giản cũng có thể mạnh mẽ.









