Suy nghĩ về Kiểm tra Mô hình
NoneCác phần sau đây trước tiên trình bày một phương pháp tiếp cận ngây thơ để xác thực mô hình và lý do tại sao nó không thành công, trước khi nghiên cứu việc sử dụng holdout sets và cross-validation để đánh giá mô hình một cách mạnh mẽ hơn.
Xác thực mô hình theo cách sai¶
Hãy chứng minh phương pháp kiểm tra ngây thơ bằng cách sử dụng dữ liệu Iris, mà chúng ta đã thấy ở phần trước.Chúng ta sẽ bắt đầu bằng cách tải dữ liệu:
from sklearn.datasets import load_irisiris = load_iris()X = iris.datay = iris.target
Tiếp theo, chúng ta lựa chọn một mô hình và các siêu tham số. Ở đây, chúng ta sẽ sử dụng một mô hình phân loại k-neighbors với n_neighbors=1.Đây là một mô hình rất đơn giản và trực quan, nó nói rằng “nhãn của một điểm chưa biết là giống với nhãn của điểm đào tạo gần nhất của nó”.
from sklearn.neighbors import KNeighborsClassifiermodel = KNeighborsClassifier(n_neighbors=1)
Sau đó chúng ta huấn luyện mô hình và sử dụng nó để dự đoán nhãn cho dữ liệu mà chúng ta đã biết:
model.fit(X, y)y_model = model.predict(X)
Mã cuối cùng, chúng ta tính toán tỷ lệ điểm được gắn nhãn đúng:
from sklearn.metrics import accuracy_scoreaccuracy_score(y, y_model)
1.0
Chúng ta thấy một điểm số độ chính xác là 1.0, điều này cho thấy 100% các điểm đã được nhãn đúng bởi mô hình của chúng ta!Nhưng liệu điểm số này thực sự đo lường độ chính xác được mong đợi hay không? Liệu chúng ta đã thật sự tìm ra một mô hình mà chúng ta mong đợi nó sẽ đúng 100% thời gian?
Như bạn có thể đã hiểu, câu trả lời là không.Trên thực tế, phương pháp này chứa một lỗi cơ bản: nó huấn luyện và đánh giá mô hình trên cùng một dữ liệu.Hơn nữa, mô hình láng giềng gần nhất là một bộ ước lượng dựa trên thực thể chỉ đơn giản lưu trữ dữ liệu huấn luyện và dự đoán nhãn bằng cách so sánh dữ liệu mới với các điểm đã lưu trữ này: trừ khi trong trường hợp chứa sẵn, nó sẽ đạt độ chính xác 100% mỗi lần!
¶Xác thực mô hình theo cách đúng đắn: Bộ dữ liệu phụ
Vậy thì cần làm gì?Một cách tốt hơn để đánh giá hiệu suất của một mô hình có thể được tìm thấy bằng cách sử dụng điều được biết đến là một tập kiểm tra: tức là, chúng ta giữ lại một phần con của dữ liệu từ việc huấn luyện mô hình, sau đó sử dụng tập kiểm tra này để kiểm tra hiệu suất của mô hình.Việc chia tách này có thể được thực hiện bằng cách sử dụng công cụ train_test_split trong Scikit-Learn:
from sklearn.cross_validation import train_test_split# split the data with 50% in each setX1, X2, y1, y2 = train_test_split(X, y, random_state=0, train_size=0.5)# fit the model on one set of datamodel.fit(X1, y1)# evaluate the model on the second set of datay2_model = model.predict(X2)accuracy_score(y2, y2_model)
0.90666666666666662
Chúng ta thấy ở đây kết quả hợp lý hơn: bộ phân loại lân cận gần nhất đạt khoảng 90% độ chính xác trên tập dữ liệu giữ lại này.Tập dữ liệu giữ lại tương tự như dữ liệu không xác định, vì mô hình chưa “trông thấy” nó trước đây.
Kiểm định mô hình qua phương pháp cross-validation¶
Một nhược điểm khi sử dụng một bộ dữ liệu làm bộ kiểm tra cho việc xác nhận mô hình là chúng ta đã mất đi một phần dữ liệu trong quá trình huấn luyện mô hình.Trong trường hợp trên, một nửa bộ dữ liệu không đóng góp vào quá trình huấn luyện mô hình!Điều này không phải là tối ưu, và có thể gây ra vấn đề – đặc biệt là nếu bộ dữ liệu huấn luyện ban đầu là nhỏ.
Một cách để giải quyết vấn đề này là sử dụng cross-validation; tức là, thực hiện một chuỗi các phù hợp trong đó mỗi tập con dữ liệu được sử dụng cả làm tập huấn luyện và tập xác nhận.Một cách trực quan, nó có thể trông như thế này:
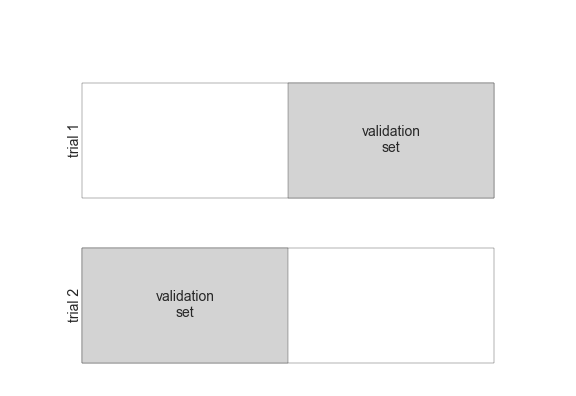
Ở đây chúng ta thực hiện hai thử nghiệm xác thực, luân phiên sử dụng mỗi nửa dữ liệu như một tập dữ liệu kiểm tra. Sử dụng dữ liệu đã chia từ trước đây, chúng ta có thể thực hiện nó như sau:
y2_model = model.fit(X1, y1).predict(X2)y1_model = model.fit(X2, y2).predict(X1)accuracy_score(y1, y1_model), accuracy_score(y2, y2_model)
(0.95999999999999996, 0.90666666666666662)
Phần này sẽ hiển thị hai điểm chính xác, mà chúng ta có thể kết hợp (bằng cách lấy trung bình) để đạt được một đo lường tốt hơn về hiệu suất tổng quát của mô hình.
Hình thức như này của cross-validation gọi là cross-validation hai lớp – có nghĩa là chúng ta đã chia dữ liệu thành hai tập và sử dụng từng tập lần lượt làm tập xác thực.
Chúng ta có thể mở rộng ý tưởng này để sử dụng thêm nhiều thử nghiệm hơn, và nhiều fold hơn trong dữ liệu – ví dụ, đây là một hình dung hình ảnh của phân chia dữ liệu theo phương pháp cross-validation tầm năm lượt:
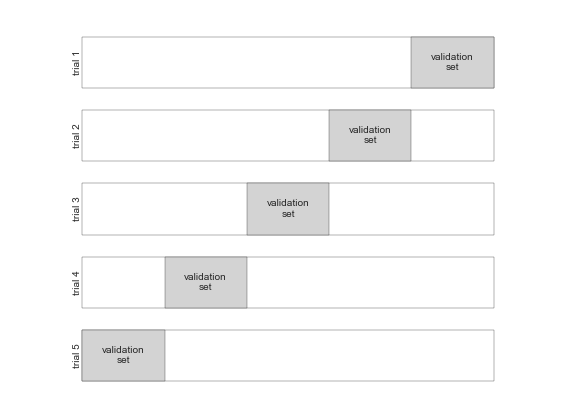
Ở đây, chúng ta chia dữ liệu thành năm nhóm và sử dụng từng nhóm lượt lượt để đánh giá sự phù hợp của mô hình trên 4/5 phần còn lại của dữ liệu.Việc này sẽ hơi rườm rà nếu thực hiện bằng tay, vì vậy chúng ta có thể sử dụng tiện ích cross_val_score của Scikit-Learn để thực hiện một cách ngắn gọn:
from sklearn.cross_validation import cross_val_scorecross_val_score(model, X, y, cv=5)
array([ 0.96666667, 0.96666667, 0.93333333, 0.93333333, 1. ])
Lặp lại việc xác nhận trên các tập con khác nhau của dữ liệu giúp chúng ta có được một ý tưởng tốt hơn về hiệu suất của thuật toán.
Scikit-Learn thực hiện một số hệ thống chia tỷ lệ xác thực chéo hữu ích trong những tình huống nhất định; những hệ thống này được thực hiện thông qua các trình lặp trong module cross_validation.Ví dụ, chúng ta có thể muốn đi đến trường hợp tới cùng trong đó số lượng vùng chia bằng với số điểm dữ liệu: nghĩa là, chúng ta huấn luyện trên tất cả các điểm nhưng chỉ còn lại một trong mỗi lần thử.Loại chia tỷ lệ xác thực chéo này được biết đến với tên gọi là leave-one-out cross validation, và có thể được sử dụng như sau:
from sklearn.cross_validation import LeaveOneOutscores = cross_val_score(model, X, y, cv=LeaveOneOut(len(X)))scores
array([ 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 0., 1., 0., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 0., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 0., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 0., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 0., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])
Do chúng ta có 150 mẫu, phương pháp cross-validation bỏ đi một mẫu được sử dụng để đánh giá với 150 lần thử, và điểm chỉ ra dự đoán thành công (1.0) hoặc không thành công (0.0).
scores.mean()
0.95999999999999996
Có thể sử dụng các phương pháp kiểm tra chéo khác tương tự như vậy.Để biết thêm về những gì có sẵn trong Scikit-Learn, sử dụng IPython để khám phá tiểu mô-đun sklearn.cross_validation, hoặc xem tài liệu trực tuyến về kiểm tra chéo của Scikit-Learn.
Lựa chọn mô hình tốt nhất¶
Bây giờ chúng ta đã thấy các khái niệm cơ bản về xác minh và xác minh chéo, chúng ta sẽ đi vào một chút sâu hơn về vấn đề lựa chọn mô hình và lựa chọn siêu tham số. Những vấn đề này là một số khía cạnh quan trọng nhất của việc thực hành máy học, và tôi thấy thường thì thông tin này thường bị bỏ qua trong các bài hướng dẫn tiếp cận về máy học sơ khai.
Điều quan trọng nhất là câu hỏi sau: nếu bộ ước lượng của chúng ta hoạt động không hiệu quả, chúng ta nên làm thế nào tiếp tục?Có một số câu trả lời có thể có:
- Sử dụng một mô hình phức tạp / linh hoạt hơn
- Sử dụng một mô hình đơn giản / linh hoạt hơn
- Tiếp thu nhiều mẫu huấn luyện hơn
- Tiếp thu nhiều dữ liệu để thêm các tính năng cho mỗi mẫu
Câu trả lời cho câu hỏi này thường là ngược lại với thiện cảm ban đầu.Đôi khi, việc sử dụng một mô hình phức tạp hơn có thể dẫn đến kết quả tồi hơn, và việc thêm nhiều dữ liệu huấn luyện hơn có thể không cải thiện kết quả của bạn!Khả năng xác định những bước nào sẽ cải thiện mô hình của bạn là điều phân biệt giữa những người thực hành học máy thành công và không thành công.
The Bias-variance trade-off¶
Cốt lõi, câu hỏi “mô hình tốt nhất” liên quan đến việc tìm điểm ngọt trong sự cân đối giữa sự thiên vị (bias) và sự biến động (variance).Xem hình dưới đây, mô tả hai kết quả hồi quy trên cùng một tập dữ liệu:
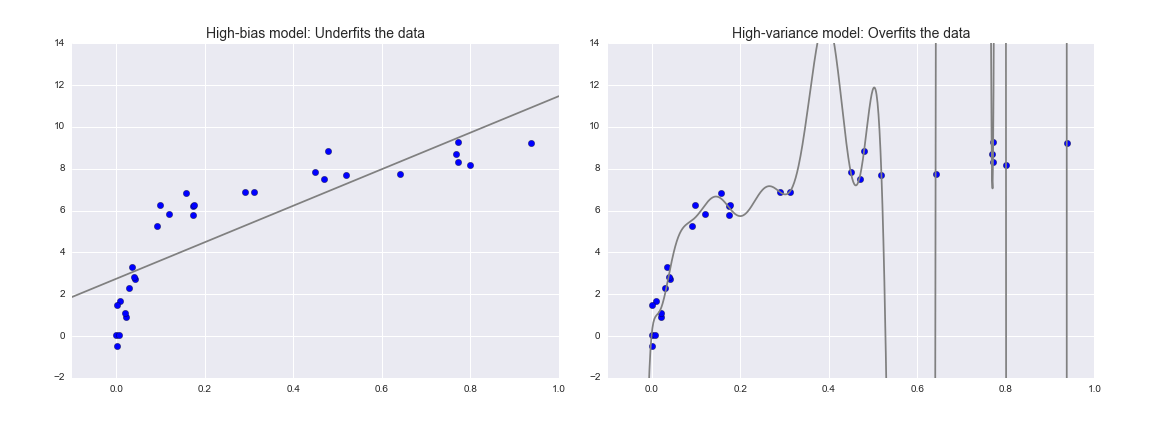
Rõ ràng là cả hai mô hình này đều không phù hợp với dữ liệu, nhưng chúng đều thất bại theo cách khác nhau.
Mô hình bên trái cố gắng tìm một đường thẳng khớp thông qua dữ liệu.Bởi vì dữ liệu intrinsically phức tạp hơn một đường thẳng, mô hình đường thẳng không bao giờ có thể mô tả tốt tập dữ liệu này.Một mô hình như vậy được gọi là underfit dữ liệu: nghĩa là, nó không có đủ linh hoạt mô hình để phù hợp với tất cả các đặc trưng trong dữ liệu; cách khác để nói điều này là mô hình có độ bias cao.
Mô hình bên phải cố gắng điều chỉnh một đa thức bậc cao thông qua dữ liệu.Ở đây, việc điều chỉnh mô hình có đủ độ linh hoạt để gần như hoàn toàn tài trợ cho các đặc điểm tốt đẹp trong dữ liệu, nhưng ngay cả khi nó mô tả một cách chính xác dữ liệu đào tạo, hình thức chính xác của nó dường như phản ánh hơn các tính chất cố hữu của quá trình nào đã tạo ra dữ liệu đó.Một mô hình như vậy được cho là overfit (quá khớp) dữ liệu: tức là, nó có quá nhiều tính linh hoạt mô hình đến mức mô hình cuối cùng chiếm một phần thông tin ngẫu nhiên cũng như phân phối dữ liệu cơ bản; một cách khác để nói điều này là mô hình có độ biến đổi cao.
Để nhìn nhận vấn đề này từ một góc độ khác, hãy xem xét những gì sẽ xảy ra nếu chúng ta sử dụng hai mô hình này để dự đoán giá trị y cho một số dữ liệu mới.Trong các sơ đồ sau đây, các điểm màu đỏ/nhạt biểu thị dữ liệu bị bỏ qua khỏi tập huấn luyện:
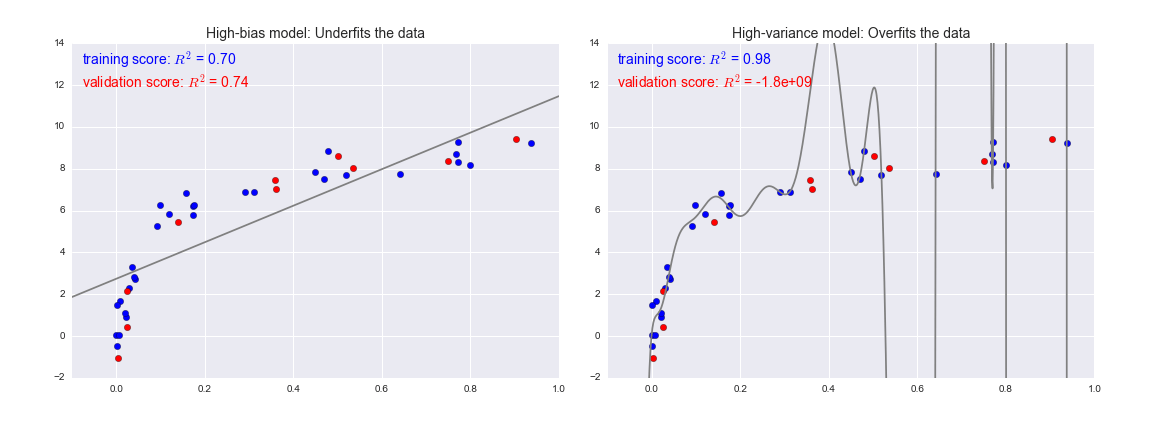
Điểm số ở đây là điểm $R^2$, hay được gọi là hệ số xác định, đo lường mức độ một mô hình thực hiện so với trung bình đơn giản của các giá trị mục tiêu. $R^2=1$ cho thấy một sự tương đồng hoàn hảo, $R^2=0$ cho thấy mô hình không tốt hơn việc chỉ lấy trung bình dữ liệu, và giá trị âm cho thấy các mô hình còn kém hơn.
NoneNếu chúng ta tưởng tượng rằng chúng ta có một số khả năng để điều chỉnh độ phức tạp của mô hình, chúng ta sẽ mong đợi điểm số huấn luyện và điểm số xác thực hoạt động như được minh họa trong hình sau:
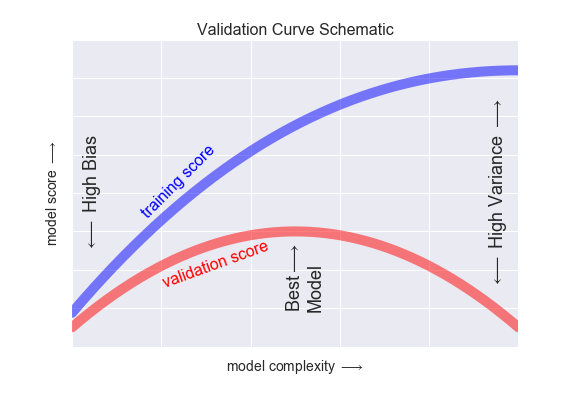
Biểu đồ được hiển thị ở đây thường được gọi là đường cong xác thực, và ta thấy các đặc điểm cần thiết sau:
- Điểm đào tạo ở mọi nơi cao hơn so với điểm xác nhận. Điều này thường xảy ra: mô hình sẽ phù hợp tốt hơn với dữ liệu mà nó đã thấy hơn là với dữ liệu mà nó chưa thấy.
- Đối với mức độ phức tạp của mô hình rất thấp (mô hình high-bias), dữ liệu đào tạo không phù hợp, có nghĩa là mô hình là một dự đoán kém cho cả dữ liệu đào tạo và dữ liệu chưa từng thấy trước đó.
- Đối với mức độ phức tạp của mô hình rất cao (mô hình high-variance), dữ liệu đào tạo bị quá trình, có nghĩa là mô hình dự đoán dữ liệu đào tạo rất tốt, nhưng thất bại đối với bất kỳ dữ liệu chưa từng thấy trước đó nào.
- Đối với một giá trị trung gian, đường cong xác nhận có một giá trị cực đại. Mức độ phức tạp này chỉ ra một sự cân nhắc thích hợp giữa sự chệch lệch và biến thiên.
Cách điều chỉnh độ phức tạp của mô hình thay đổi từ mô hình này sang mô hình khác; khi chúng tôi thảo luận chi tiết về từng mô hình ở các phần sau, chúng tôi sẽ thấy mỗi mô hình cho phép điều chỉnh như vậy.
Các đường cong xác thực trong Scikit-Learn¶
Hãy xem ví dụ về việc sử dụng cross-validation để tính toán đường cong xác thực cho một lớp các mô hình.Ở đây chúng ta sẽ sử dụng một mô hình hồi quy đa thức: đây là một mô hình tuyến tính tổng quát trong đó bậc của đa thức là một tham số có thể điều chỉnh.Ví dụ, một đa thức bậc 1 phù hợp với một đường thẳng cho dữ liệu; với các tham số mô hình $a$ và $b$:
$$y = ax + b$$
Một đa thức bậc 3 phù hợp với đường cong hình học bất kỳ; đối với các tham số mô hình $a, b, c, d$:
$$y = ax^3 + bx^2 + cx + d$$
Chúng ta có thể tổng quát hóa điều này cho bất kỳ số lượng đặc trưng đa thức nào.Trong Scikit-Learn, chúng ta có thể thực hiện điều này bằng một linear regression đơn giản kết hợp với bộ xử lý đa thức.Chúng ta sẽ sử dụng một pipeline để kết hợp các hoạt động này thành một chuỗi (chúng ta sẽ thảo luận về đặc trưng đa thức và pipeline chi tiết hơn trong Feature Engineering):
from sklearn.preprocessing import PolynomialFeaturesfrom sklearn.linear_model import LinearRegressionfrom sklearn.pipeline import make_pipelinedef PolynomialRegression(degree=2, **kwargs): return make_pipeline(PolynomialFeatures(degree), LinearRegression(**kwargs))
Bây giờ chúng ta hãy tạo một số dữ liệu mà chúng ta sẽ sử dụng để đưa vào mô hình của chúng ta:
import numpy as npdef make_data(N, err=1.0, rseed=1): # randomly sample the data rng = np.random.RandomState(rseed) X = rng.rand(N, 1) ** 2 y = 10 - 1. / (X.ravel() + 0.1) if err > 0: y += err * rng.randn(N) return X, yX, y = make_data(40)
Bây giờ chúng ta có thể hiển thị dữ liệu của mình, cùng với các đường cong đa thức của một số bậc:
%matplotlib inlineimport matplotlib.pyplot as pltimport seaborn; seaborn.set() # plot formattingX_test = np.linspace(-0.1, 1.1, 500)[:, None]plt.scatter(X.ravel(), y, color='black')axis = plt.axis()for degree in [1, 3, 5]: y_test = PolynomialRegression(degree).fit(X, y).predict(X_test) plt.plot(X_test.ravel(), y_test, label='degree={0}'.format(degree))plt.xlim(-0.1, 1.0)plt.ylim(-2, 12)plt.legend(loc='best');

Chiếc núm điều khiển sự phức tạp của mô hình trong trường hợp này là mức độ của đa thức, có thể là bất kỳ số nguyên không âm nào.Một câu hỏi hữu ích cần được trả lời là: mức độ đa thức nào cung cấp một sự cân đối phù hợp giữa sai lệch (không phù hợp với dữ liệu) và phương sai (quá khớp)?
Chúng ta có thể tiến bộ trong việc này bằng cách trực quan hóa đường cong kiểm định cho dữ liệu và mô hình cụ thể này; điều này có thể được thực hiện một cách dễ dàng bằng cách sử dụng tiện ích validation_curve được cung cấp bởi Scikit-Learn.Cho một mô hình, dữ liệu, tên tham số và một phạm vi để khám phá, hàm này sẽ tự động tính toán cả điểm học tập và điểm kiểm định trên phạm vi:
from sklearn.learning_curve import validation_curvedegree = np.arange(0, 21)train_score, val_score = validation_curve(PolynomialRegression(), X, y, 'polynomialfeatures__degree', degree, cv=7)plt.plot(degree, np.median(train_score, 1), color='blue', label='training score')plt.plot(degree, np.median(val_score, 1), color='red', label='validation score')plt.legend(loc='best')plt.ylim(0, 1)plt.xlabel('degree')plt.ylabel('score');
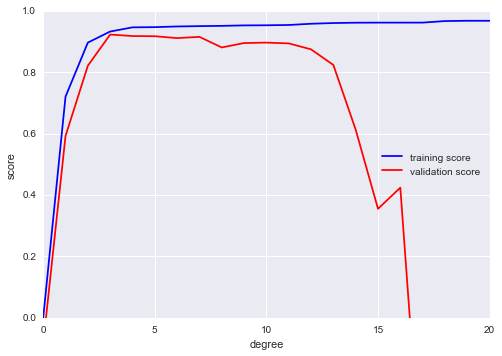
Đoạn mã HTML trên cho thấy chính xác hành vi chất lượng chúng tôi mong đợi: điểm đào tạo luôn cao hơn so với điểm xác thực; điểm đào tạo liên tục cải thiện với sự phức tạp mô hình tăng lên; và điểm xác thực đạt đến mức tối đa trước khi giảm dần khi mô hình trở nên quá khớp.
Từ đường cong xác nhận, chúng ta có thể đọc được rằng sự cân đối tốt nhất giữa độ lệch và phương sai được tìm thấy cho một đa thức bậc ba; chúng ta có thể tính toán và hiển thị bộ khớp này trên dữ liệu gốc như sau:
plt.scatter(X.ravel(), y)lim = plt.axis()y_test = PolynomialRegression(3).fit(X, y).predict(X_test)plt.plot(X_test.ravel(), y_test);plt.axis(lim);
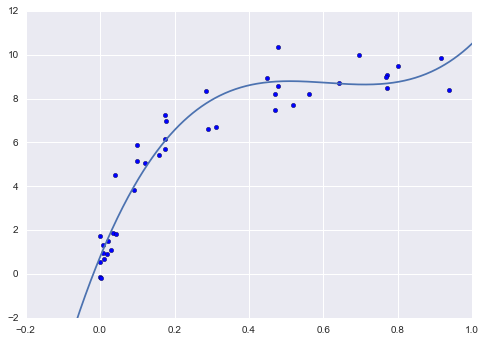
Chú ý rằng việc tìm kiếm mô hình tối ưu này thực sự không yêu cầu chúng ta tính điểm huấn luyện, nhưng xem xét mối quan hệ giữa điểm huấn luyện và điểm xác thực có thể mang lại cho chúng ta những hiểu biết hữu ích về hiệu suất của mô hình.
Đường cong học tập¶
Một khía cạnh quan trọng của độ phức tạp của mô hình là mô hình tối ưu thường phụ thuộc vào kích thước dữ liệu huấn luyện của bạn.Ví dụ, hãy tạo một bộ dữ liệu mới với một tỷ lệ nhân lên năm lần:
X2, y2 = make_data(200)plt.scatter(X2.ravel(), y2);
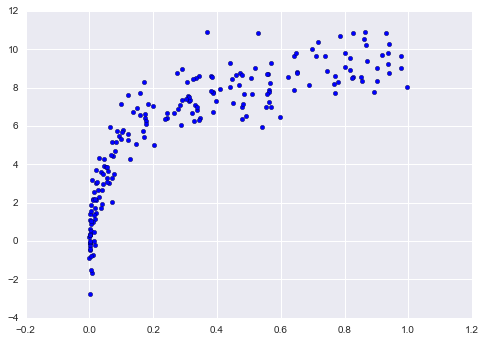
Chúng ta sẽ nhân đôi mã trước để vẽ đồ thị đường cong xác thực cho tập dữ liệu lớn hơn này; cho mục đích tham chiếu, hãy vẽ lại kết quả trước đó:
degree = np.arange(21)train_score2, val_score2 = validation_curve(PolynomialRegression(), X2, y2, 'polynomialfeatures__degree', degree, cv=7)plt.plot(degree, np.median(train_score2, 1), color='blue', label='training score')plt.plot(degree, np.median(val_score2, 1), color='red', label='validation score')plt.plot(degree, np.median(train_score, 1), color='blue', alpha=0.3, linestyle='dashed')plt.plot(degree, np.median(val_score, 1), color='red', alpha=0.3, linestyle='dashed')plt.legend(loc='lower center')plt.ylim(0, 1)plt.xlabel('degree')plt.ylabel('score');
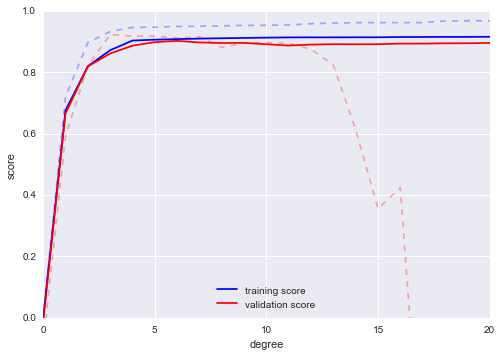
Các đường solid (đậm) cho thấy những kết quả mới, trong khi các đường dashed (nhạt) chỉ ra kết quả của những tập dữ liệu nhỏ trước đó.Dễ thấy từ biểu đồ validation curve rằng tập dữ liệu lớn hỗ trợ một mô hình phức tạp hơn rất nhiều: bởi đỉnh của đường này có thể là xấp xỉ mức 6, nhưng ngay cả một mô hình degree-20 cũng không mắc phải over-fit nghiêm trọng dữ liệu – validation score và training score vẫn rất gần nhau.
Ngay từ đầu, chúng ta đã nhận thấy rằng hành vi của đường cong xác thực không chỉ có một mà hai yếu tố quan trọng: độ phức tạp của mô hình và số lượng điểm huấn luyện.Thường thì việc khám phá hành vi của mô hình dựa trên số lượng điểm huấn luyện là rất hữu ích, điều này có thể được thực hiện bằng cách sử dụng các tập con ngày càng lớn hơn của dữ liệu để điều chỉnh mô hình của chúng ta.Một biểu đồ về điểm số huấn luyện/xác thực liên quan đến kích thước của tập huấn luyện được biết đến là một đường cong học tập.
Hành vi chung mà chúng ta mong đợi từ đường cong học là như sau:
- Một mô hình phức tạp sẽ “overfit” một bộ dữ liệu nhỏ: điều này có nghĩa là điểm số huấn luyện sẽ cao, trong khi điểm số xác thực sẽ thấp.
- Một mô hình có độ phức tạp nhất định sẽ “underfit” một bộ dữ liệu lớn: điều này có nghĩa là điểm số huấn luyện sẽ giảm, nhưng điểm số xác thực sẽ tăng.
- Một mô hình sẽ không bao giờ, trừ khi tình cờ, cho điểm số tốt hơn cho bộ xác thực so với bộ huấn luyện: điều này có nghĩa là đường cong nên tiếp tục gần nhau nhưng không bao giờ giao nhau.
Với những tính năng này trong tâm trí, chúng tôi mong đợi đường cong học tập sẽ có dạng như hình minh họa sau:
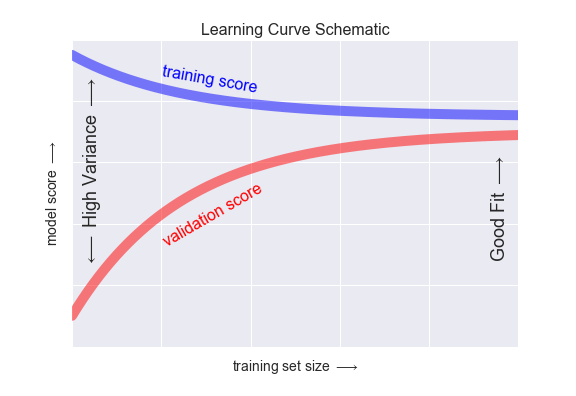
Một đặc điểm đáng chú ý của đồ thị học tập là sự hội tụ về một điểm số cụ thể khi số lượng mẫu huấn luyện tăng lên.Đặc biệt, khi đã có đủ điểm để một mô hình nhất định hội tụ, thêm dữ liệu huấn luyện sẽ không giúp ích cho bạn!Cách duy nhất để nâng cao hiệu suất của mô hình trong trường hợp này là sử dụng một mô hình khác (thường là phức tạp hơn).
Learning curves in Scikit-Learn¶
Scikit-Learn cung cấp một tiện ích thuận tiện để tính toán các đường cong học tập từ mô hình của bạn; ở đây chúng tôi sẽ tính toán một đường cong học tập cho bộ dữ liệu gốc của chúng tôi với một mô hình đa thức bậc hai và một mô hình đa thức bậc chín:
from sklearn.learning_curve import learning_curvefig, ax = plt.subplots(1, 2, figsize=(16, 6))fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1)for i, degree in enumerate([2, 9]): N, train_lc, val_lc = learning_curve(PolynomialRegression(degree), X, y, cv=7, train_sizes=np.linspace(0.3, 1, 25)) ax[i].plot(N, np.mean(train_lc, 1), color='blue', label='training score') ax[i].plot(N, np.mean(val_lc, 1), color='red', label='validation score') ax[i].hlines(np.mean([train_lc[-1], val_lc[-1]]), N[0], N[-1], color='gray', linestyle='dashed') ax[i].set_ylim(0, 1) ax[i].set_xlim(N[0], N[-1]) ax[i].set_xlabel('training size') ax[i].set_ylabel('score') ax[i].set_title('degree = {0}'.format(degree), size=14) ax[i].legend(loc='best')
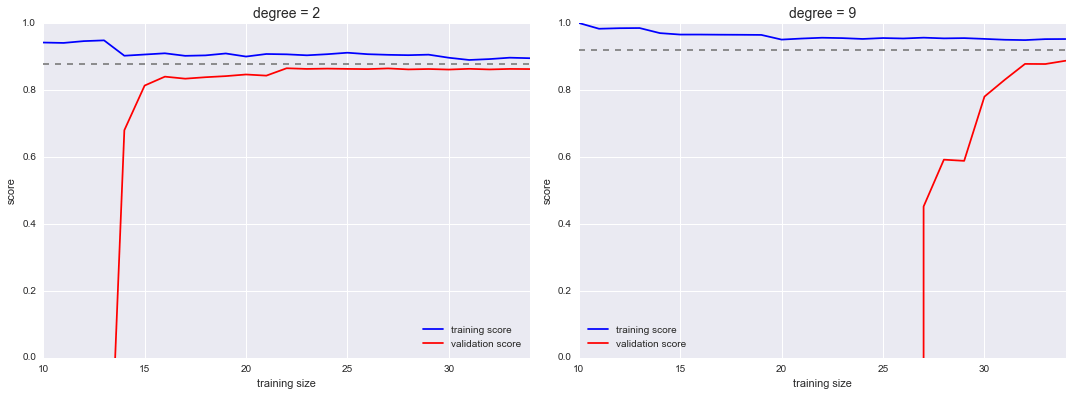
Đây là một thông tin chẩn đoán quý giá, bởi vì nó cho chúng ta một hình ảnh minh họa về cách mà mô hình của chúng ta phản ứng với việc tăng dữ liệu huấn luyện.
Cách duy nhất để tăng điểm hội tụ là sử dụng một mô hình khác (thường là phức tạp hơn).Chúng ta có thể thấy điều này ở bảng bên phải: bằng cách chuyển sang một mô hình phức tạp hơn, chúng ta tăng điểm số hội tụ (được chỉ bởi đường kẻ đứt), nhưng đồng thời làm tăng phương sai của mô hình (được chỉ bởi sự khác biệt giữa điểm số huấn luyện và xác thực).Nếu chúng ta thêm nhiều điểm dữ liệu hơn, đường học tập cho mô hình phức tạp sẽ cuối cùng hội tụ.
Vẽ đồ thị học tập (learning curve) cho lựa chọn mô hình và tập dữ liệu của bạn cụ thể có thể giúp bạn đưa ra quyết định về cách tiến lên trong việc cải thiện phân tích của bạn.
Ứng dụng thực tiễn của việc xác thực: Tìm kiếm theo lưới¶
Đoạn thảo luận trước nhằm mang lại cho bạn một số hiểu biết về sự cân đối giữa sai lệch và phương sai, và sự phụ thuộc của nó vào sự phức tạp của mô hình và kích thước tập huấn luyện.Trong thực tế, các mô hình thông thường có nhiều hẹn đề để điều chỉnh, và do đó biểu đồ của các đường viền kiểm tra và học tập sẽ thay đổi từ đường thẳng thành các bề mặt đa chiều.Trong những trường hợp như vậy, các hình ảnh hóa đó là khó khăn và chúng tôi sẽ muốn đơn giản hóa việc tìm ra mô hình cụ thể nào tạo ra điểm số thông qua việc kiểm tra tối đa hóa.
Scikit-Learn cung cấp các công cụ tự động để làm việc này trong mô-đun tìm kiếm lưới.Dưới đây là một ví dụ về việc sử dụng tìm kiếm lưới để tìm mô hình đa thức tối ưu.Chúng ta sẽ khám phá một lưới ba chiều của các đặc trưng của mô hình; gồm bậc đa thức, cờ cho chúng ta biết liệu có vừa vào, và cờ cho chúng ta biết liệu có chuẩn hóa vấn đề.Điều này có thể được thiết lập bằng meta-estimator GridSearchCV của Scikit-Learn:
from sklearn.grid_search import GridSearchCVparam_grid = {'polynomialfeatures__degree': np.arange(21), 'linearregression__fit_intercept': [True, False], 'linearregression__normalize': [True, False]}grid = GridSearchCV(PolynomialRegression(), param_grid, cv=7)
Chú ý rằng giống như một bộ ước lượng thông thường, việc này chưa được áp dụng vào bất kỳ dữ liệu nào.Gọi phương thức fit() sẽ thích ứng mô hình tại mỗi điểm lưới, theo dõi các điểm số trên đường đi:
grid.fit(X, y);
Bây giờ khi điều này đã phù hợp, chúng ta có thể yêu cầu các thông số tốt nhất như sau:
grid.best_params_
{'linearregression__fit_intercept': False, 'linearregression__normalize': True, 'polynomialfeatures__degree': 4}
Cuối cùng, nếu chúng ta muốn, chúng ta có thể sử dụng mô hình tốt nhất và hiển thị sự khớp với dữ liệu của chúng ta bằng cách sử dụng mã từ trước:
model = grid.best_estimator_plt.scatter(X.ravel(), y)lim = plt.axis()y_test = model.fit(X, y).predict(X_test)plt.plot(X_test.ravel(), y_test, hold=True);plt.axis(lim);
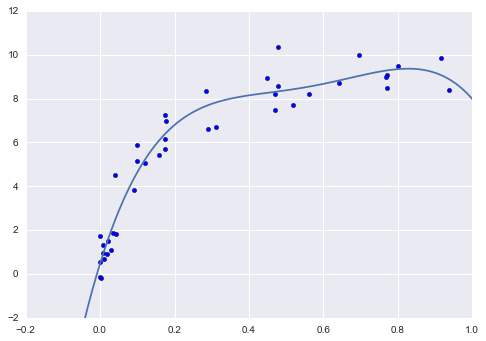
Công cụ tìm kiếm lưới cung cấp nhiều tùy chọn hơn, bao gồm khả năng chỉ định một hàm điểm tùy chỉnh, để song song hóa các tính toán, để thực hiện tìm kiếm ngẫu nhiên và nhiều hơn nữa.
Tóm tắt¶
Trong phần này, chúng ta đã bắt đầu khám phá khái niệm xác thực mô hình và tối ưu hoá siêu tham số, tập trung vào các khía cạnh thông thường của sự cân bằng giữa độ lệch và phương sai và cách nó ảnh hưởng khi cài đặt các mô hình cho dữ liệu.Cụ thể, chúng ta nhận thấy việc sử dụng tập xác thực hoặc phương pháp chéo xác thực là rất quan trọng khi điều chỉnh các tham số để tránh quá khớp đối với các mô hình phức tạp/tích hợp.
Trong các phần tiếp theo, chúng ta sẽ thảo luận về các mô hình hữu ích đặc biệt và trong suốt sẽ nói về điều chỉnh nào có sẵn cho những mô hình này và cách những tham số không giới hạn này ảnh hưởng đến độ phức tạp của mô hình.Hãy ghi nhớ những bài học trong phần này khi bạn tiếp tục đọc và tìm hiểu về những phương pháp học máy này!









