Hồi quy tuyến tính đơn giản¶
Chúng ta sẽ bắt đầu với phương pháp hồi quy tuyến tính phổ biến nhất, đó là một đường thẳng cơ bản phù hợp với dữ liệu.Phương pháp hồi quy tuyến tính mô hình một đường thẳng theo công thức$$y = ax + b$$trong đó $a$ thường được gọi là hệ số góc, và $b$ thường được gọi là hệ số chặn.
Xét dữ liệu sau đây, nó được phân tán trên một đường thẳng với độ dốc là 2 và tiếp tuyến là -5:
rng = np.random.RandomState(1)x = 10 * rng.rand(50)y = 2 * x - 5 + rng.randn(50)plt.scatter(x, y);
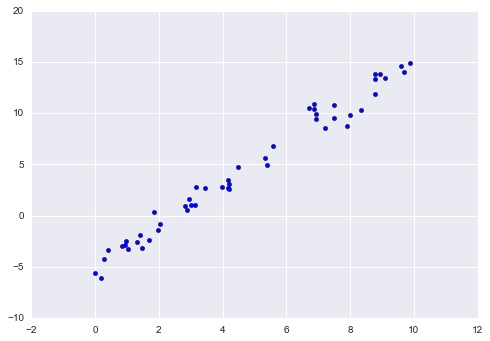
Chúng ta có thể sử dụng bộ xử lý LinearRegression của Scikit-Learn để khớp dữ liệu này và xây dựng đường thẳng phù hợp nhất:
from sklearn.linear_model import LinearRegressionmodel = LinearRegression(fit_intercept=True)model.fit(x[:, np.newaxis], y)xfit = np.linspace(0, 10, 1000)yfit = model.predict(xfit[:, np.newaxis])plt.scatter(x, y)plt.plot(xfit, yfit);
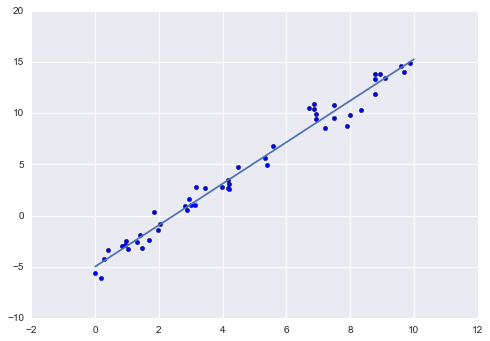
Xuống dòng và góc nghiêng của dữ liệu được chứa trong các parameter phù hợp của mô hình, trong Scikit-Learn thì luôn được đánh dấu bởi dấu gạch chân cuối cùng.
print("Model slope: ", model.coef_[0])print("Model intercept:", model.intercept_)
Model slope: 2.02720881036Model intercept: -4.99857708555
Chúng ta thấy rằng kết quả rất gần với các đầu vào, như chúng ta có thể mong đợi.
Estimator LinearRegression có khả năng mạnh mẽ hơn nhiều so với việc đơn giản chỉ sử dụng các đường thẳng, nó còn có thể xử lý các mô hình tuyến tính đa chiều dạng$$y = a_0 + a_1 x_1 + a_2 x_2 + \cdots$$trong đó có nhiều giá trị $x$.Hình học, điều này tương tự như việc đưa một mặt phẳng cho các điểm trong không gian ba chiều hoặc đưa một siêu mặt phẳng cho các điểm trong không gian nhiều chiều hơn.
Tính chất đa chiều của các phương trình hồi quy như vậy làm cho chúng khó hình dung hơn, nhưng chúng ta có thể thấy một trong những sự phù hợp này đang hoạt động bằng cách xây dựng một số dữ liệu ví dụ, sử dụng toán tử nhân ma trận của NumPy:
rng = np.random.RandomState(1)X = 10 * rng.rand(100, 3)y = 0.5 + np.dot(X, [1.5, -2., 1.])model.fit(X, y)print(model.intercept_)print(model.coef_)
0.5[ 1.5 -2. 1. ]
Ở đây, dữ liệu $y$ được xây dựng từ ba giá trị ngẫu nhiên $x$, và phương trình hồi quy tuyến tính khôi phục lại các hệ số được sử dụng để xây dựng dữ liệu.
Theo cách này, chúng ta có thể sử dụng bộ ước lượng viên tuyến tính đơn LinearRegression để phù hợp với các đường, các mặt phẳng hoặc siêu mặt phẳng đến dữ liệu của chúng ta.Dường như phương pháp này sẽ bị giới hạn chỉ đối với các mối quan hệ tuyến tính giữa các biến, nhưng hóa ra chúng ta cũng có thể có những điều này một cách linh hoạt.
Hồi quy Hàm Cơ Bản¶
Một mẹo bạn có thể sử dụng để áp dụng hồi quy tuyến tính cho mối quan hệ phi tuyến giữa các biến là biến đổi dữ liệu theo hàm cơ sở.Chúng ta đã thấy một phiên bản của điều này trước đó, trong ống dẫn PolynomialRegression được sử dụng trong Hyperparameters and Model Validation và Feature Engineering.Ý tưởng là lấy mô hình tuyến tính đa chiều của chúng ta:$$y = a_0 + a_1 x_1 + a_2 x_2 + a_3 x_3 + \cdots$$và xây dựng $x_1, x_2, x_3,$ và các thành phần khác từ đầu vào một chiều duy nhất của chúng ta $x$.Nghĩa là, chúng ta cho phép $x_n = f_n(x)$, trong đó $f_n()$ là một hàm biến đổi dữ liệu của chúng ta.
Ví dụ, nếu $f_n(x) = x^n$, mô hình của chúng ta trở thành một đa thức hồi quy:$$y = a_0 + a_1 x + a_2 x^2 + a_3 x^3 + \cdots$$Lưu ý rằng đây vẫn là một mô hình tuyến tính — tính tuyến tính liên quan đến việc hệ số $a_n$ không nhân hoặc chia cho nhau.Những gì chúng ta đã thực hiện hiệu quả là lấy các giá trị $x$ một chiều của chúng ta và chiếu chúng vào một số chiều cao hơn, để một mô hình tuyến tính có thể vừa khớp với mối quan hệ phức tạp hơn giữa $x$ và $y$.
Hàm cơ sở đa thức¶
Phép chiếu đa thức này rất hữu ích nên nó được tích hợp vào Scikit-Learn, sử dụng bộ biến đổi PolynomialFeatures:
from sklearn.preprocessing import PolynomialFeaturesx = np.array([2, 3, 4])poly = PolynomialFeatures(3, include_bias=False)poly.fit_transform(x[:, None])
array([[ 2., 4., 8.], [ 3., 9., 27.], [ 4., 16., 64.]])
Chúng ta thấy ở đây rằng bộ biến đổi đã chuyển đổi mảng một chiều của chúng ta thành một mảng ba chiều bằng cách lấy lũy thừa của mỗi giá trị.Bản biểu diễn dữ liệu mới, có số chiều cao hơn, sau đó có thể được đưa vào một phương trình hồi quy tuyến tính.
Như chúng ta đã thấy trong Feature Engineering, cách tốt nhất để làm điều này là sử dụng một pipeline.Hãy tạo một mô hình đa thức bậc 7 theo cách này:
from sklearn.pipeline import make_pipelinepoly_model = make_pipeline(PolynomialFeatures(7), LinearRegression())
Với việc áp dụng biến đổi này, chúng ta có thể sử dụng mô hình tuyến tính để phù hợp với mối quan hệ phức tạp hơn giữa $x$ và $y$.Ví dụ, đây là một sóng sine có nhiễu:
rng = np.random.RandomState(1)x = 10 * rng.rand(50)y = np.sin(x) + 0.1 * rng.randn(50)poly_model.fit(x[:, np.newaxis], y)yfit = poly_model.predict(xfit[:, np.newaxis])plt.scatter(x, y)plt.plot(xfit, yfit);
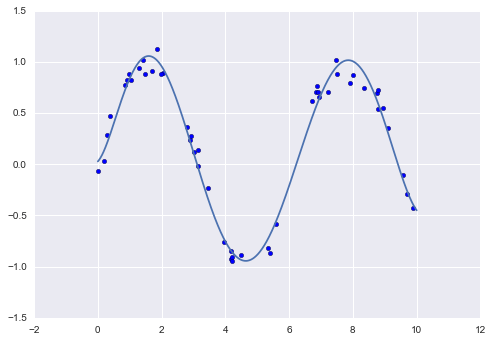
Mô hình tuyến tính của chúng tôi, thông qua việc sử dụng các hàm cơ sở đa thức bậc 7, có thể cung cấp một sự phù hợp tuyệt vời với dữ liệu phi tuyến này!
Hàm cơ sở Gaussian¶
Tất nhiên, có thể sử dụng các hàm cơ sở khác.Ví dụ, một mẫu hữu ích khác là sử dụng một mô hình không phải là tổng các hàm cơ sở đa thức, mà là tổng các hàm cơ sở Gaussian.Kết quả có thể trông giống như hình dưới đây:
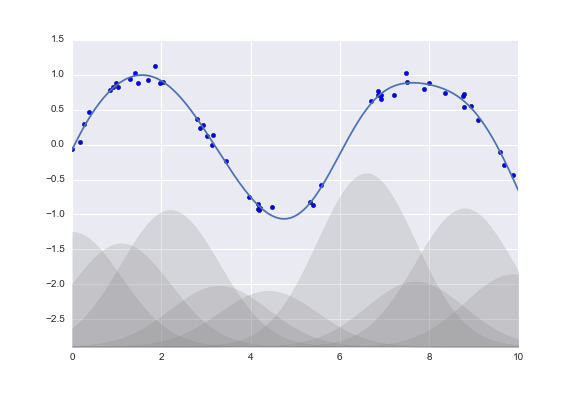
Các vùng đã được tô màu trên đồ thị là các hàm cơ sở đã được tỉ lệ, và khi cộng lại chúng tạo ra đường cong mượt qua dữ liệu.Các hàm cơ sở Gaussian này không được tích hợp sẵn trong Scikit-Learn, nhưng chúng ta có thể viết một bộ biến đổi tùy chỉnh để tạo ra chúng, như được thể hiện ở đây và minh họa trong hình sau (các bộ biến đổi của Scikit-Learn được cài đặt dưới dạng các lớp Python; đọc mã nguồn của Scikit-Learn là một cách tốt để xem cách chúng có thể được tạo ra):
from sklearn.base import BaseEstimator, TransformerMixinclass GaussianFeatures(BaseEstimator, TransformerMixin): """Uniformly spaced Gaussian features for one-dimensional input""" def __init__(self, N, width_factor=2.0): self.N = N self.width_factor = width_factor @staticmethod def _gauss_basis(x, y, width, axis=None): arg = (x - y) / width return np.exp(-0.5 * np.sum(arg ** 2, axis)) def fit(self, X, y=None): # create N centers spread along the data range self.centers_ = np.linspace(X.min(), X.max(), self.N) self.width_ = self.width_factor * (self.centers_[1] - self.centers_[0]) return self def transform(self, X): return self._gauss_basis(X[:, :, np.newaxis], self.centers_, self.width_, axis=1) gauss_model = make_pipeline(GaussianFeatures(20), LinearRegression())gauss_model.fit(x[:, np.newaxis], y)yfit = gauss_model.predict(xfit[:, np.newaxis])plt.scatter(x, y)plt.plot(xfit, yfit)plt.xlim(0, 10);
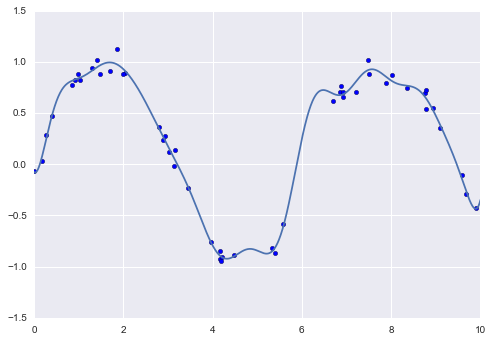
Chúng tôi đặt ví dụ này ở đây chỉ để làm rõ rằng không có gì phép thuật về các hàm cơ sở đa thức: nếu bạn có một loại thông minh nào đó vào quá trình tạo ra dữ liệu của bạn mà khiến bạn nghĩ rằng một cơ sở hay một cái khác có thể thích hợp, bạn cũng có thể sử dụng chúng.
Regularization¶
Sự giới thiệu của các hàm cơ sở vào phương trình hồi quy tuyến tính của chúng ta làm cho mô hình linh hoạt hơn nhiều, nhưng nó cũng có thể dẫn đến tình trạng quá khớp một cách nhanh chóng (xem lại Siêu tham số và Xác thực Mô hình để có một cuộc thảo luận về vấn đề này).Ví dụ, nếu chúng ta chọn quá nhiều hàm cơ sở Gaussian, chúng ta sẽ có kết quả không tốt:
model = make_pipeline(GaussianFeatures(30), LinearRegression())model.fit(x[:, np.newaxis], y)plt.scatter(x, y)plt.plot(xfit, model.predict(xfit[:, np.newaxis]))plt.xlim(0, 10)plt.ylim(-1.5, 1.5);
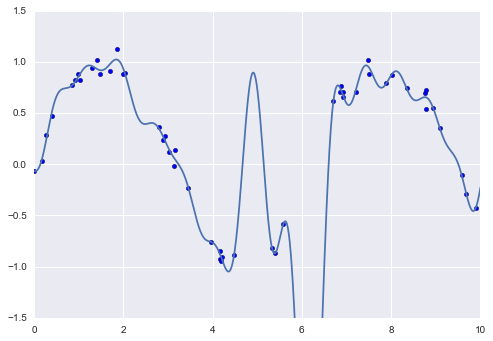
Với dữ liệu được chiếu lên cơ sở 30 chiều, mô hình có quá nhiều tính linh hoạt và đi qua các giá trị tới cực đại giữa các vị trí mà nó bị ràng buộc bởi dữ liệu.Chúng ta có thể nhìn thấy lý do cho điều này nếu chúng ta vẽ đồ thị hệ số của các cơ sở Gaussian theo vị trí của chúng:
def basis_plot(model, title=None): fig, ax = plt.subplots(2, sharex=True) model.fit(x[:, np.newaxis], y) ax[0].scatter(x, y) ax[0].plot(xfit, model.predict(xfit[:, np.newaxis])) ax[0].set(xlabel='x', ylabel='y', ylim=(-1.5, 1.5)) if title: ax[0].set_title(title) ax[1].plot(model.steps[0][1].centers_, model.steps[1][1].coef_) ax[1].set(xlabel='basis location', ylabel='coefficient', xlim=(0, 10)) model = make_pipeline(GaussianFeatures(30), LinearRegression())basis_plot(model)
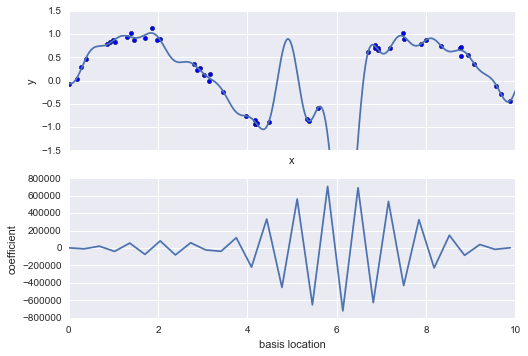
Phần dưới của hình ảnh này hiển thị độ lớn của hàm cơ sở tại mỗi vị trí.Đây là hành vi quá khớp thông thường khi các hàm cơ sở chồng lên nhau: hệ số của các hàm cơ sở kề nhau tăng lên và đối phó lẫn nhau.Chúng ta biết rằng những hành vi như vậy gây rủi ro và tốt hơn nếu chúng ta có thể giới hạn những điểm cao như vậy một cách rõ ràng trong mô hình bằng cách trừ phạt các giá trị lớn của các tham số mô hình.Hình phạt như vậy được biết đến là chính quy hóa và có nhiều hình thức.
Ridge regression (Điều chỉnh $L_2$)¶
Có lẽ hình thức thông thường nhất của regularization được biết đến là ridge regression hay $L_2$ regularization, đôi khi còn được gọi là Tikhonov regularization. Điều này thực hiện bằng cách trừ tiếp tục tổng bình phương (2-norms) của các hệ số mô hình; trong trường hợp này, hình phạt trên mô hình phù hợp sẽ là $$ P = \alpha\sum_{n=1}^N \theta_n^2 $$ trong đó $\alpha$ là một tham số tự do điều khiển mức độ hình phạt. Loại mô hình có hình phạt này được tích hợp sẵn trong Scikit-Learn với bộ ước lượng Ridge:
from sklearn.linear_model import Ridgemodel = make_pipeline(GaussianFeatures(30), Ridge(alpha=0.1))basis_plot(model, title='Ridge Regression')
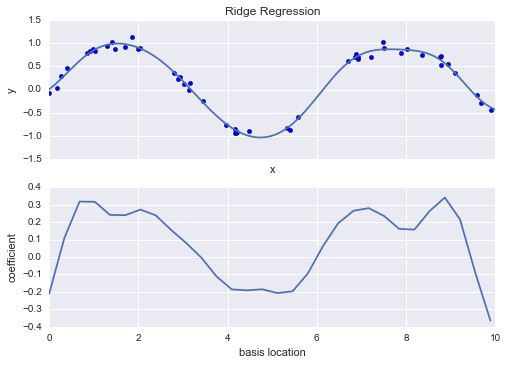
Tham số $\alpha$ là một cái núm điều chỉnh sự phức tạp của mô hình kết quả.Trong giới hạn $\alpha \to 0$, chúng ta khôi phục kết quả hồi quy tuyến tính thông thường; trong giới hạn $\alpha \to \infty$, tất cả các đáp ứng của mô hình sẽ bị ngăn chặn.Một lợi thế đặc biệt của hồi quy ridge là nó có thể tính toán rất hiệu quả – gần như không tốn thêm chi phí tính toán so với mô hình hồi quy tuyến tính ban đầu.
Lasso regression ($L_1$ regularization)¶
Một dạng chính của việc điều chuẩn thông thường khác được biết đến là lasso và liên quan đến việc phạt tổng giá trị tuyệt đối (1-norm) của các hệ số hồi quy:$$P = \alpha\sum_{n=1}^N |\theta_n|$$Mặc dù điều này từ mặt khái niệm tương tự với hồi quy ridge, kết quả có thể khác bất ngờ: ví dụ, do lý do hình học, hồi quy lasso thường ưa thích mô hình thưa thớt liệu có thể: nghĩa là, nó ưu tiên đặt các hệ số mô hình thành chính xác bằng không.
Chúng ta có thể thấy hành vi này khi nhân đôi hình ảnh của hồi quy ridge, nhưng sử dụng hệ số đã được chuẩn hóa L1:
from sklearn.linear_model import Lassomodel = make_pipeline(GaussianFeatures(30), Lasso(alpha=0.001))basis_plot(model, title='Lasso Regression')
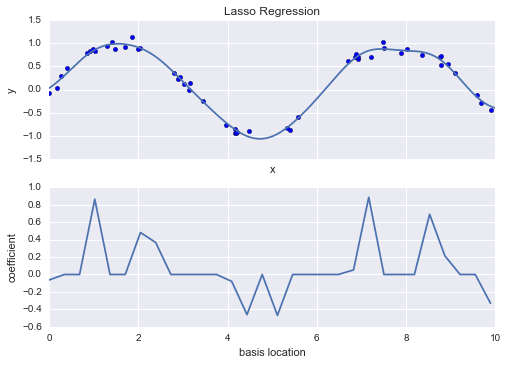
Với hình phạt lasso regression, đa số các hệ số đều là chính xác bằng không, với hành vi chức năng được mô phỏng bởi một tập hợp con nhỏ của các hàm cơ sở có sẵn.Tương tự như regularization ridge, tham số $\alpha$ điều chỉnh công suất của hình phạt, và nên được xác định thông qua, ví dụ, cross-validation (tham khảo Hyperparameters and Model Validation để biết thêm thông tin).
Ví dụ: Dự đoán giao thông xe đạp¶
Như một ví dụ, hãy xem xét xem chúng ta có thể dự đoán số lượt đi xe đạp qua Cầu Fremont ở Seattle dựa trên thời tiết, mùa và các yếu tố khác.
Trong phần này, chúng ta sẽ kết hợp dữ liệu về xe đạp với một tập dữ liệu khác và cố gắng xác định mức độ mà yếu tố thời tiết và mùa vụ – nhiệt độ, lượng mưa và số giờ ánh sáng ban ngày – ảnh hưởng đến lưu lượng giao thông xe đạp qua con đường này.May mắn thay, NOAA cung cấp dữ liệu thời tiết hàng ngày của các trạm của họ tại đây (tôi đã sử dụng mã trạm USW00024233) và chúng ta có thể dễ dàng sử dụng Pandas để kết hợp hai nguồn dữ liệu này.Chúng tôi sẽ thực hiện một phép hồi quy tuyến tính đơn giản để liên kết thông tin về thời tiết và các thông số khác với số lượng đếm xe đạp, để ước tính cách thay đổi trong bất kỳ một trong những tham số này ảnh hưởng đến số lượng người đi xe trong một ngày cụ thể.
Riêng biệt, đây là ví dụ về cách các công cụ của Scikit-Learn có thể được sử dụng trong một khung mô hình hóa thống kê, trong đó các tham số của mô hình được cho là có ý nghĩa có thể giải thích được.Như đã thảo luận trước đây, đây không phải là một phương pháp tiêu chuẩn trong học máy, nhưng sự giải thích như vậy là có thể đối với một số mô hình.
Bắt đầu bằng cách tải hai tập dữ liệu, lập chỉ mục theo ngày:
# !curl -o FremontBridge.csv https://data.seattle.gov/api/views/65db-xm6k/rows.csv?accessType=DOWNLOAD
import pandas as pdcounts = pd.read_csv('FremontBridge.csv', index_col='Date', parse_dates=True)weather = pd.read_csv('data/BicycleWeather.csv', index_col='DATE', parse_dates=True)
Tiếp theo chúng ta sẽ tính toán tổng lưu lượng xe đạp hàng ngày và đặt nó vào một khung dữ liệu riêng:
daily = counts.resample('d').sum()daily['Total'] = daily.sum(axis=1)daily = daily[['Total']] # remove other columns
Chúng ta đã thấy trước đó rằng các mẫu sử dụng thường thay đổi từ ngày này sang ngày khác; hãy lưu trữ điều này trong dữ liệu của chúng ta bằng cách thêm cột nhị phân chỉ ra ngày trong tuần:
days = ['Mon', 'Tue', 'Wed', 'Thu', 'Fri', 'Sat', 'Sun']for i in range(7): daily[days[i]] = (daily.index.dayofweek == i).astype(float)
Tương tự, chúng ta có thể mong đợi các tay đua có thái độ khác biệt vào các ngày lễ; hãy thêm một chỉ báo cho điều này:
from pandas.tseries.holiday import USFederalHolidayCalendarcal = USFederalHolidayCalendar()holidays = cal.holidays('2012', '2016')daily = daily.join(pd.Series(1, index=holidays, name='holiday'))daily['holiday'].fillna(0, inplace=True)
Chúng ta cũng có thể nghi ngờ rằng số giờ nắng sẽ ảnh hưởng đến số người đi xe; hãy sử dụng tính toán thiên văn tiêu chuẩn để bổ sung thông tin này:
def hours_of_daylight(date, axis=23.44, latitude=47.61): """Compute the hours of daylight for the given date""" days = (date - pd.datetime(2000, 12, 21)).days m = (1. - np.tan(np.radians(latitude)) * np.tan(np.radians(axis) * np.cos(days * 2 * np.pi / 365.25))) return 24. * np.degrees(np.arccos(1 - np.clip(m, 0, 2))) / 180.daily['daylight_hrs'] = list(map(hours_of_daylight, daily.index))daily[['daylight_hrs']].plot()plt.ylim(8, 17)
(8, 17)
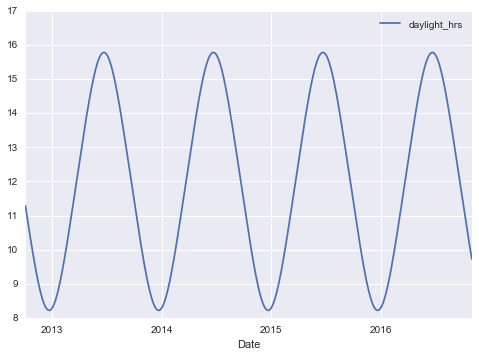
Chúng ta cũng có thể thêm nhiệt độ trung bình và tổng lượng mưa vào dữ liệu.Ngoài lượng mưa tính bằng inch, hãy thêm một cờ hiệu cho biết liệu một ngày có khô (có lượng mưa bằng không) hay không:
# temperatures are in 1/10 deg C; convert to Cweather['TMIN'] /= 10weather['TMAX'] /= 10weather['Temp (C)'] = 0.5 * (weather['TMIN'] + weather['TMAX'])# precip is in 1/10 mm; convert to inchesweather['PRCP'] /= 254weather['dry day'] = (weather['PRCP'] == 0).astype(int)daily = daily.join(weather[['PRCP', 'Temp (C)', 'dry day']])
Cuối cùng, chúng ta hãy thêm một đếm ngược mà tăng lên từ ngày 1, và đo số năm đã trôi qua.Điều này sẽ cho phép chúng ta đo bất kỳ sự tăng hoặc giảm hàng năm nào trong số xe qua cầu hàng ngày đã quan sát:
daily['annual'] = (daily.index - daily.index[0]).days / 365.
Bây giờ dữ liệu của chúng ta đã được sắp xếp, và chúng ta có thể nhìn vào nó:
daily.head()
Với điều này, chúng ta có thể chọn các cột để sử dụng và phù hợp mô hình hồi quy tuyến tính vào dữ liệu của chúng ta.Chúng ta sẽ đặt fit_intercept = False, vì các biến cờ hàng ngày thực tế là các intercept riêng biệt cho từng ngày của chúng:
# Drop any rows with null valuesdaily.dropna(axis=0, how='any', inplace=True)column_names = ['Mon', 'Tue', 'Wed', 'Thu', 'Fri', 'Sat', 'Sun', 'holiday', 'daylight_hrs', 'PRCP', 'dry day', 'Temp (C)', 'annual']X = daily[column_names]y = daily['Total']model = LinearRegression(fit_intercept=False)model.fit(X, y)daily['predicted'] = model.predict(X)
Sau cùng, chúng ta có thể so sánh giao thông xe đạp tổng hợp và dự đoán theo cách trực quan:
daily[['Total', 'predicted']].plot(alpha=0.5);
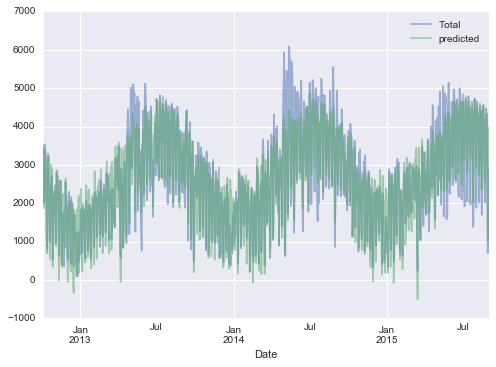
Rõ ràng rằng chúng ta đã bỏ qua một số tính năng quan trọng, đặc biệt trong mùa hè.Hoặc là các tính năng của chúng ta không hoàn chỉnh (tức là người ta quyết định liệu có đi làm bằng xe đạp dựa trên nhiều yếu tố khác ngoài những yếu tố này) hoặc có một số mối quan hệ phi tuyến mà chúng ta đã bỏ qua (ví dụ, có thể người ta đi xe ít hơn ở cả nhiệt độ cao và thấp).Tuy nhiên, xấp xỉ đơn giản của chúng ta đủ để cung cấp cho chúng ta một số thông tin, và chúng ta có thể xem các hệ số của mô hình tuyến tính để ước tính mức đóng góp của từng tính năng vào số lượt xe đạp hàng ngày:
params = pd.Series(model.coef_, index=X.columns)params
Mon 504.882756Tue 610.233936Wed 592.673642Thu 482.358115Fri 177.980345Sat -1103.301710Sun -1133.567246holiday -1187.401381daylight_hrs 128.851511PRCP -664.834882dry day 547.698592Temp (C) 65.162791annual 26.942713dtype: float64
Các số này khó để hiểu được mà không có một phép đo không chắc chắn nào cả.Chúng ta có thể tính toán những sự không chắc chắn này nhanh chóng bằng cách lấy mẫu lại dữ liệu bằng phương pháp bootstrap:
from sklearn.utils import resamplenp.random.seed(1)err = np.std([model.fit(*resample(X, y)).coef_ for i in range(1000)], 0)
Với các lỗi này được ước tính, hãy xem lại kết quả:
print(pd.DataFrame({'effect': params.round(0), 'error': err.round(0)}))
effect errorMon 505.0 86.0Tue 610.0 83.0Wed 593.0 83.0Thu 482.0 85.0Fri 178.0 81.0Sat -1103.0 80.0Sun -1134.0 83.0holiday -1187.0 163.0daylight_hrs 129.0 9.0PRCP -665.0 62.0dry day 548.0 33.0Temp (C) 65.0 4.0annual 27.0 18.0
Ta thấy rằng có một xu hướng tương đối ổn định trong chu kỳ hàng tuần: có nhiều người đi xe vào các ngày trong tuần hơn vào cuối tuần hay ngày lễ.Ta thấy rằng với mỗi giờ ánh sáng ban ngày thêm, có 129 ± 9 người biết đến việc chọn xe đạp để di chuyển thêm; mỗi độ C tăng thêm trong nhiệt độ khí hậu thì có 65 ± 4 người cầm xe đạp đi; một ngày không mưa có nghĩa là trung bình có thêm 548 ± 33 người sẽ sử dụng xe đạp và mỗi inch nước mưa có nghĩa là cỡ 665 ± 62 người không đi xe.Một khi ta tính toán tất cả các yếu tố này, ta thấy mỗi năm có thêm 27 ± 18 người đi xe hàng ngày.
Mô hình của chúng ta hầu hết chắc chắn thiếu một số thông tin liên quan. Ví dụ, hiệu ứng phi tuyến (như hiệu ứng của mưa và nhiệt độ lạnh) và xu hướng phi tuyến bên trong mỗi biến (như sự không sẵn lòng đi xe ở nhiệt độ rất lạnh và nhiệt độ rất nóng) không thể được tính đến trong mô hình này.Ngoài ra, chúng ta đã bỏ bớt một số thông tin tinh vi hơn (như sự khác biệt giữa buổi sáng mưa và buổi chiều mưa) và chúng ta đã bỏ qua sự tương quan giữa các ngày (như hiệu ứng có thể của một ngày thứ Ba mưa đối với số liệu của Thứ Tư, hoặc hiệu ứng của một ngày nắng bất ngờ sau một chuỗi những ngày mưa).Đây là những hiệu ứng có thể hấp dẫn và bạn hiện đã có công cụ để bắt đầu khám phá chúng nếu bạn muốn!










