Biểu diễn Dữ liệu trong Scikit-Learn¶
Máy học là về việc tạo ra các mô hình từ dữ liệu: vì lí do đó, chúng tôi sẽ bắt đầu bằng việc thảo luận về cách biểu diễn dữ liệu để máy tính hiểu.
Dữ liệu dưới dạng bảng¶
Một bảng cơ bản là một lưới hai chiều của dữ liệu, trong đó các hàng đại diện cho các phần tử cá nhân của tập dữ liệu, và các cột đại diện cho các lượng liên quan đến mỗi phần tử này.Ví dụ, hãy xem xét bộ dữ liệu hoa Iris, được nghiên cứu nổi tiếng bởi Ronald Fisher vào năm 1936.Chúng ta có thể tải xuống bộ dữ liệu này dưới dạng một DataFrame của Pandas bằng cách sử dụng thư viện seaborn:
import seaborn as snsiris = sns.load_dataset('iris')iris.head()
Ở đây, mỗi hàng trong dữ liệu tương ứng với một bông hoa được quan sát, và số lượng hàng chính là tổng số bông hoa trong bộ dữ liệu.Nói chung, chúng ta sẽ gọi các hàng của ma trận là mẫu, và số lượng hàng sẽ được gọi là n_samples.
Tương tự, mỗi cột của dữ liệu tham chiếu đến một đặc điểm lượng tử cụ thể mô tả mỗi mẫu.
Bảng đặc điểm¶
Bảng này mô tả rõ ràng rằng thông tin có thể được coi như một mảng số hai chiều hoặc ma trận, mà chúng ta sẽ gọi là features matrix. Theo quy ước, features matrix này thường được lưu trữ trong một biến có tên là X. Features matrix được giả định là hai chiều, với hình dạng là [n_samples, n_features], và thường được chứa trong một mảng NumPy hoặc một DataFrame của Pandas, mặc dù một số mô hình Scikit-Learn cũng chấp nhận ma trận thưa thớt SciPy.
Các ví dụ (tức là các hàng) luôn liên quan đến các đối tượng cá nhân mô tả bởi tập dữ liệu.Ví dụ, ví dụ có thể là một bông hoa, một người, một tài liệu, một hình ảnh, một tập tin âm thanh, một video, một vật thể thiên văn, hoặc bất cứ thứ gì khác bạn có thể mô tả bằng một tập hợp các đo đạc số lượng.
Các tính năng (tức là cột) luôn đề cập đến các quan sát riêng biệt mô tả mỗi mẫu một cách định lượng.Các tính năng thường có giá trị thực, nhưng trong một số trường hợp có thể là giá trị Boolean hoặc rời rạc.
Mảng mục tiêu¶
Ngoài bảng tính năng X, chúng ta cũng thường làm việc với một mảng nhãn hoặc mảng mục tiêu, theo quy ước chúng ta thường gọi là y.Mảng mục tiêu thường có một chiều, có độ dài n_samples, và thường được chứa trong một mảng NumPy hoặc Series của Pandas.Mảng mục tiêu có thể có giá trị số liên tục hoặc các lớp/nhãn rời rạc.Mặc dù một số bộ ước lượng Scikit-Learn xử lý nhiều giá trị mục tiêu dưới dạng mảng mục tiêu hai chiều, [n_samples, n_targets], chúng ta thường làm việc chủ yếu với trường hợp phổ biến của mảng mục tiêu một chiều.
Thường một điểm gây nhầm lẫn là cách mảng đích khác biệt so với các cột đặc trưng khác. Đặc điểm phân biệt của mảng đích là nó thường là số lượng chúng ta muốn dự đoán từ dữ liệu: trong thuật ngữ thống kê, đó là biến phụ thuộc.Ví dụ, trong dữ liệu trước đó, chúng ta có thể muốn xây dựng một mô hình có thể dự đoán loài hoa dựa trên các đo lường khác; trong trường hợp này, cột species sẽ được coi là mảng đích.
Với mục tiêu mảng này trong tâm trí, chúng ta có thể sử dụng Seaborn (xem Hiển thị dữ liệu bằng Seaborn) để thuận tiện hóa việc trực quan hóa dữ liệu:
%matplotlib inlineimport seaborn as sns; sns.set()sns.pairplot(iris, hue='species', size=1.5);
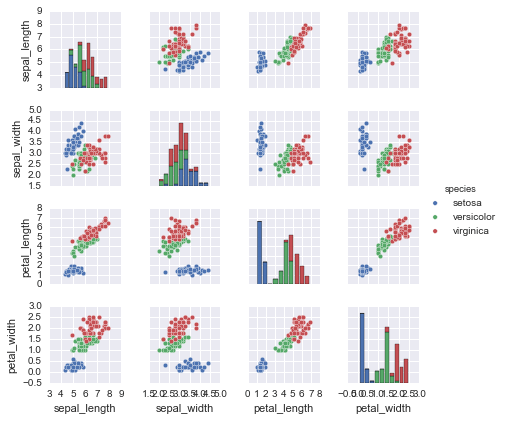
Để sử dụng trong Scikit-Learn, chúng ta sẽ trích xuất ma trận đặc trưng và mảng mục tiêu từ DataFrame, điều này chúng ta có thể thực hiện bằng cách sử dụng một số thao tác DataFrame của Pandas đã được thảo luận trong Chương 3:
X_iris = iris.drop('species', axis=1)X_iris.shape
(150, 4)
y_iris = iris['species']y_iris.shape
(150,)
Để tóm tắt, cấu trúc dự kiến của các tính năng và giá trị mục tiêu được hình dung trong sơ đồ sau:
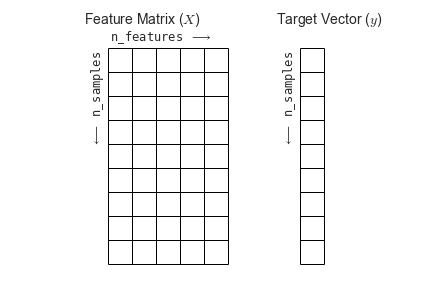
Với dữ liệu này được định dạng đúng cách, chúng ta có thể tiếp tục xem xét API của bộ ước lượng trong Scikit-Learn:
Giao diện Estimator trong Scikit-Learn¶
API của Scikit-Learn được thiết kế dựa trên các nguyên tắc hướng dẫn sau, được trình bày trong bài báo API của Scikit-Learn này:
Khả năng nhất quán: Tất cả các đối tượng chia sẻ một giao diện chung được lấy ra từ một tập hợp giới hạn các phương thức, với tài liệu nhất quán.
Công cụ kiểm tra: Tất cả các giá trị tham số được chỉ định được công khai như các thuộc tính công khai.
Sự hạn chế về cây hệ thống đối tượng: Chỉ có các thuật toán được đại diện bởi các lớp Python; các tập dữ liệu được đại diệnbằng các định dạng tiêu chuẩn (mảng NumPy,
DataFramecủa Pandas, ma trận thưa thớt SciPy) và tên tham sốsử dụng các chuỗi Python tiêu chuẩn.Tổ hợp: Nhiều nhiệm vụ học máy có thể được biểu diễn dưới dạng các chuỗi các thuật toán cơ bản hơn,và Scikit-Learn sử dụng điều này bất cứ lúc nào có thể.
Cài đặt hợp lý: Khi các mô hình yêu cầu các tham số được người dùng chỉ định, thư viện xác định một giá trị mặc định phù hợp.
Tính nhất quán: Tất cả các đối tượng chia sẻ một giao diện chung được lấy từ một tập hợp hữu hạn các phương thức, với tài liệu nhất quán.
Kiểm tra: Tất cả các giá trị tham số được chỉ định được hiển thị như các thuộc tính công khai.
Hệ thống phân cấp đối tượng hạn chế: Chỉ có các thuật toán được biểu diễn bằng các lớp Python; các tập dữ liệu được biểu diễn dưới các định dạng tiêu chuẩn (mảng NumPy, các DataFrame của Pandas, ma trận thưa rải của SciPy) và các tên tham số sử dụng chuỗi Python tiêu chuẩn.
Tái bút giả: Nhiều nhiệm vụ học máy có thể được diễn tả dưới dạng các chuỗi của các thuật toán cơ bản hơn,và Scikit-Learn sử dụng điều này mỗi khi có thể.
Các giá trị mặc định hợp lý: Khi các mô hình yêu cầu các tham số do người dùng xác định, thư viện xác định một giá trị mặc định phù hợp.
Trong thực tế, những nguyên tắc này giúp Scikit-Learn trở nên rất dễ sử dụng, sau khi đã hiểu được những nguyên tắc cơ bản.Mọi thuật toán học máy trong Scikit-Learn được thực hiện thông qua Estimator API, cung cấp một giao diện nhất quán cho một loạt các ứng dụng học máy.
Cơ bản của API¶
Thường thì, các bước trong việc sử dụng API mô phỏng Scikit-Learn như sau (chúng ta sẽ đi qua một số ví dụ chi tiết trong các phần tiếp theo).
- Chọn một lớp mô hình bằng cách nhập lớp ước lượng viên thích hợp từ Scikit-Learn.
- Chọn siêu tham số mô hình bằng cách khởi tạo lớp này với các giá trị mong muốn.
- Sắp xếp dữ liệu thành ma trận đặc trưng và vectơ mục tiêu theo thảo luận ở trên.
- Phù hợp mô hình với dữ liệu của bạn bằng cách gọi phương thức
fit()của thể hiện mô hình. - Áp dụng Mô hình cho dữ liệu mới:
- Đối với học có giám sát, thường chúng ta dự đoán nhãn cho dữ liệu không biết bằng cách sử dụng phương thức
predict(). - Đối với học không giám sát, chúng ta thường biến đổi hoặc suy ra các thuộc tính của dữ liệu bằng cách sử dụng các phương thức
transform()hoặcpredict().
- Đối với học có giám sát, thường chúng ta dự đoán nhãn cho dữ liệu không biết bằng cách sử dụng phương thức
- Đối với học có giám sát, chúng ta thường dự đoán nhãn cho dữ liệu chưa biết bằng cách sử dụng phương thức
predict(). - Đối với học không giám sát, chúng ta thường biến đổi hoặc suy ra các thuộc tính của dữ liệu bằng cách sử dụng phương thức
transform()hoặcpredict().
Bây giờ chúng ta sẽ đi qua một số ví dụ đơn giản về việc áp dụng các phương pháp học có giám sát và học không giám sát.
Ví dụ về học có giám sát: Hồi quy tuyến tính đơn giản¶
Như một ví dụ về quá trình này, hãy xem xét một phương trình hồi quy tuyến tính đơn giản- nghĩa là trường hợp phổ biến của việc điều chỉnh đường thẳng cho dữ liệu $(x, y)$.Chúng tôi sẽ sử dụng dữ liệu đơn giản sau đây cho ví dụ về hồi quy của chúng ta:
import matplotlib.pyplot as pltimport numpy as nprng = np.random.RandomState(42)x = 10 * rng.rand(50)y = 2 * x - 1 + rng.randn(50)plt.scatter(x, y);
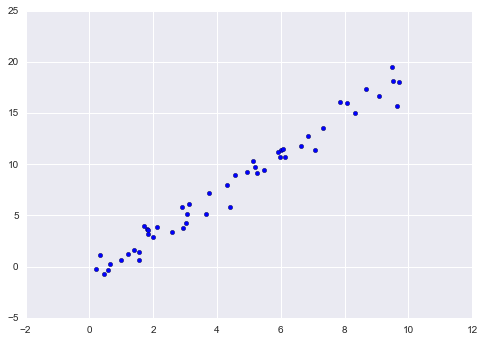
Với dữ liệu này đã được đặt vào chỗ, chúng ta có thể sử dụng công thức được đề cập trước đó. Hãy đi qua quá trình này:
1. Chọn một lớp mô-đun¶
Trong Scikit-Learn, mỗi loại mô hình được biểu diễn bằng một lớp Python.Vì vậy, ví dụ, nếu chúng ta muốn tính toán một mô hình hồi quy tuyến tính đơn giản, chúng ta có thể nhập lớp hồi quy tuyến tính:
from sklearn.linear_model import LinearRegression
Lưu ý rằng còn tồn tại các mô hình hồi quy tuyến tính phổ biến khác; bạn có thể đọc thêm về chúng trong tài liệu mô-đun sklearn.linear_model của gói sklearn.
2. Chọn tham số mạng¶
Một điểm quan trọng là một lớp mô hình không giống như một trường hợp của một mô hình.
Một khi chúng ta đã quyết định về lớp model của mình, vẫn còn một số lựa chọn mở cho chúng ta.Tùy thuộc vào lớp model mà chúng ta đang làm việc, chúng ta có thể cần trả lời một hoặc nhiều câu hỏi như sau:
- Chúng ta có muốn điều chỉnh offset (tức là điểm cắt với trục y) không?
- Chúng ta có muốn chuẩn hóa mô hình không?
- Chúng ta có muốn tiền xử lý các đặc trưng để tăng tính linh hoạt của mô hình không?
- Chúng ta muốn sử dụng mức độ điều chỉnh như thế nào trong mô hình?
- Chúng ta muốn sử dụng bao nhiêu thành phần mô hình?
Đây là những ví dụ về các lựa chọn quan trọng phải được thực hiện một khi đã chọn lớp mô hình.Những lựa chọn này thường được đại diện là tham số siêu, hoặc các tham số phải được thiết lập trước khi mô hình được phù hợp với dữ liệu.Trong Scikit-Learn, tham số siêu được chọn bằng cách chuyển giá trị vào khi khởi tạo mô hình.Chúng ta sẽ tìm hiểu cách bạn có thể logic với số liệu chọn lựa tham số siêu trong Tham số Siêu và Đánh giá Mô hình.
Đối với ví dụ về hồi quy tuyến tính của chúng ta, chúng ta có thể khởi tạo lớp LinearRegression và chỉ định rằng chúng ta muốn điều chỉnh đường chéo (intercept) bằng cách sử dụng siêu tham số fit_intercept:
model = LinearRegression(fit_intercept=True)model
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
Hãy nhớ rằng khi mô hình được khởi tạo, việc duy nhất là lưu trữ các giá trị của các tham số siêu (hyperparameter) này.Đặc biệt, chúng ta chưa áp dụng mô hình lên bất kỳ dữ liệu nào: giao diện lập trình ứng dụng (API) Scikit-Learn cho thấy rõ ràng sự khác biệt giữa lựa chọn mô hình và áp dụng mô hình lên dữ liệu.
3. Sắp xếp dữ liệu vào một features matrix và target vector¶
Trước đó, chúng tôi đã chi tiết các biểu diễn dữ liệu của Scikit-Learn, yêu cầu một ma trận đặc trưng hai chiều và một mảng mục tiêu một chiều.
X = x[:, np.newaxis]X.shape
(50, 1)
4. Điều chỉnh mô hình cho dữ liệu của bạn¶
Bây giờ là thời điểm để áp dụng mô hình của chúng ta vào dữ liệu.Điều này có thể được thực hiện bằng phương thức fit() của mô hình:
model.fit(X, y)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
Lệnh fit() này gây ra một số tính toán nội bộ phụ thuộc vào từng mô hình, và kết quả của những tính toán này được lưu trong các thuộc tính cụ thể cho từng mô hình mà người dùng có thể khám phá.Trong Scikit-Learn, theo quy ước, tất cả các tham số mô hình đã học trong quá trình fit() đều có dấu gạch chân ở cuối; ví dụ, trong mô hình tuyến tính này, chúng ta có những tham số sau:
model.coef_
array([ 1.9776566])
model.intercept_
-0.90331072553111635
Hai tham số này đại diện cho độ dốc và giao điểm của phù hợp tuyến tính đơn giản với dữ liệu.So sánh với định nghĩa dữ liệu, chúng ta thấy chúng rất gần với độ dốc nhập vào là 2 và giao điểm là -1.
Một câu hỏi thường xuyên đặt ra liên quan đến sự không chắc chắn trong các tham số mô hình nội bộ như vậy.Nói chung, Scikit-Learn không cung cấp các công cụ để rút ra kết luận từ các tham số mô hình nội bộ: việc diễn giải các tham số mô hình là một câu hỏi mô hình thống kê hơn là một câu hỏi học máy.Học máy thay vào đó tập trung vào điều mô hình dự đoán.Nếu bạn muốn đào sâu vào ý nghĩa của các tham số phù hợp trong mô hình, có sẵn các công cụ khác, bao gồm Gói Statsmodels Python.
5. Dự đoán nhãn cho dữ liệu chưa biết¶
Khi mô hình đã được huấn luyện, nhiệm vụ chính của học máy có giám sát là đánh giá nó dựa trên những gì nó nói về dữ liệu mới mà không phải là một phần của bộ dữ liệu huấn luyện.Trong Scikit-Learn, điều này có thể được thực hiện bằng cách sử dụng phương thức predict().Vì mục đích của ví dụ này, “dữ liệu mới” của chúng tôi sẽ là một lưới các giá trị x, và chúng tôi sẽ hỏi mô hình dự đoán giá trị y nào:
xfit = np.linspace(-1, 11)
Như trước đây, chúng ta cần ép buộc các giá trị x này thành ma trận đặc trưng [n_samples, n_features], sau đó chúng ta có thể đưa nó vào model:
Xfit = xfit[:, np.newaxis]yfit = model.predict(Xfit)
Một ngày cuối cùng, hãy hình dung kết quả bằng cách vẽ đồ thị trước với dữ liệu gốc, và sau đó là mô hình đã được cải thiện:
plt.scatter(x, y)plt.plot(xfit, yfit);
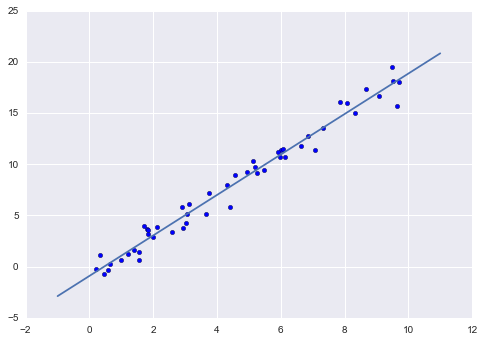
Thường các hiệu suất của mô hình được đánh giá bằng cách so sánh kết quả của nó với một giá trị cơ sở đã biết, như chúng ta sẽ thấy trong ví dụ tiếp theo
Ví dụ về học có giám sát: Phân loại Iris¶
Hãy xem một ví dụ khác về quy trình này, sử dụng bộ dữ liệu Iris mà chúng ta đã thảo luận trước đây.Câu hỏi của chúng ta sẽ là: với một mô hình được huấn luyện trên một phần của dữ liệu Iris, chúng ta có thể dự đoán nhãn còn lại như thế nào?
Đối với nhiệm vụ này, chúng ta sẽ sử dụng một mô hình sinh ra cực kỳ đơn giản được gọi là Gaussian naive Bayes, mô hình này tiến hành bằng cách cho rằng mỗi lớp được rút ra từ phân phối Gaussian thẳng đứng (xem Chi tiết: Phân loại Naive Bayes để biết thêm chi tiết).Bởi vì nó rất nhanh và không có siêu tham số để chọn, Gaussian naive Bayes thường là một mô hình tốt để sử dụng như một điểm chuẩn cho phân loại, trước khi khám phá xem liệu có thể tìm thấy cải tiến thông qua các mô hình phức tạp hơn.
Chúng ta muốn đánh giá mô hình trên dữ liệu mà nó chưa từng thấy, do đó chúng ta sẽ chia dữ liệu thành một tập huấn luyện và một tập kiểm tra.Việc này có thể được thực hiện bằng cách thủ công, nhưng việc sử dụng hàm tiện ích train_test_split là thuận tiện hơn:
from sklearn.cross_validation import train_test_splitXtrain, Xtest, ytrain, ytest = train_test_split(X_iris, y_iris, random_state=1)
Với dữ liệu được sắp xếp, chúng ta có thể tuân theo công thức để dự đoán các nhãn:
from sklearn.naive_bayes import GaussianNB # 1. choose model classmodel = GaussianNB() # 2. instantiate modelmodel.fit(Xtrain, ytrain) # 3. fit model to datay_model = model.predict(Xtest) # 4. predict on new data
Một công cụ cấp thẻ accuracy_score cuối cùng cũng có thể được sử dụng để xem tỷ lệ phân loại nhãn dự đoán khớp với giá trị thực tế của chúng:
from sklearn.metrics import accuracy_scoreaccuracy_score(ytest, y_model)
0.97368421052631582
Với một độ chính xác vượt trội 97%, chúng ta thấy rằng ngay cả thuật toán phân loại rất ngây thơ này cũng hiệu quả đối với tập dữ liệu cụ thể này!
Bài toán học phi tuyến Iris: khối lưỡng¶
Như một ví dụ về một vấn đề học không giám sát, hãy xem xét việc giảm chiều của dữ liệu Iris để dễ dàng hơn khi trực quan hóa nó.Nhớ rằng dữ liệu Iris có bốn chiều: có bốn thuộc tính được ghi lại cho mỗi mẫu.
Nhiệm vụ của việc giảm số chiều dữ liệu là xem xét xem có một biểu diễn chiều dữ liệu thấp hơn phù hợp giữ được các đặc trưng cần thiết của dữ liệu hay không.Thường thì việc giảm số chiều được sử dụng như là một phương tiện hỗ trợ để trực quan hóa dữ liệu: vì sau cùng, việc vẽ đồ thị dữ liệu trong hai chiều dễ dàng hơn so với bốn chiều hoặc cao hơn!
Ở đây chúng ta sẽ sử dụng phân tích thành phần chính (PCA; xem Sâu hơn: Phân tích thành phần chính), đây là một kỹ thuật giảm chiều dữ liệu tuyến tính nhanh chóng.Chúng ta sẽ yêu cầu mô hình trả về hai thành phần – tức là một biểu diễn hai chiều của dữ liệu.
Theo thứ tự các bước được trình bày trước đó, chúng ta có:
from sklearn.decomposition import PCA # 1. Choose the model classmodel = PCA(n_components=2) # 2. Instantiate the model with hyperparametersmodel.fit(X_iris) # 3. Fit to data. Notice y is not specified!X_2D = model.transform(X_iris) # 4. Transform the data to two dimensions
Bây giờ chúng ta hãy vẽ biểu đồ kết quả. Một cách nhanh chóng để làm điều này là chèn kết quả vào DataFrame ban đầu của Iris và sử dụng lmplot của Seaborn để hiển thị kết quả:
iris['PCA1'] = X_2D[:, 0]iris['PCA2'] = X_2D[:, 1]sns.lmplot("PCA1", "PCA2", hue='species', data=iris, fit_reg=False);
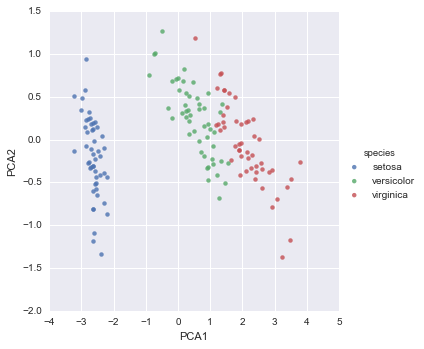
Ta thấy rằng trong biểu diễn hai chiều, các loài được phân tách tương đối tốt, mặc dù thuật toán PCA không biết về các nhãn loài!Điều này cho thấy việc phân loại tương đối đơn giản sẽ có hiệu quả trên tập dữ liệu, như chúng ta đã thấy trước đó.
Học không giám sát: Phân cụm Iris¶
Hãy tiếp tục xem xét việc áp dụng phân cụm cho dữ liệu Iris.Một thuật toán phân cụm cố gắng tìm ra nhóm dữ liệu khác biệt mà không liên quan đến bất kỳ nhãn nào.Ở đây, chúng ta sẽ sử dụng một phương pháp phân cụm mạnh mẽ được gọi là mô hình hỗn hợp Gaussian (GMM), được thảo luận chi tiết hơn trong Chi tiết: Mô hình hỗn hợp Gaussian.Một mô hình GMM cố gắng mô phỏng dữ liệu như một tập hợp các blob Gaussian.
Chúng ta có thể thực hiện việc áp dụng mô hình hỗn hợp Gaussian như sau:
from sklearn.mixture import GMM # 1. Choose the model classmodel = GMM(n_components=3, covariance_type='full') # 2. Instantiate the model with hyperparametersmodel.fit(X_iris) # 3. Fit to data. Notice y is not specified!y_gmm = model.predict(X_iris) # 4. Determine cluster labels
Như đã trước, chúng ta sẽ thêm nhãn cụm vào Iris DataFrame và sử dụng Seaborn để vẽ biểu đồ kết quả:
iris['cluster'] = y_gmmsns.lmplot("PCA1", "PCA2", data=iris, hue='species', col='cluster', fit_reg=False);
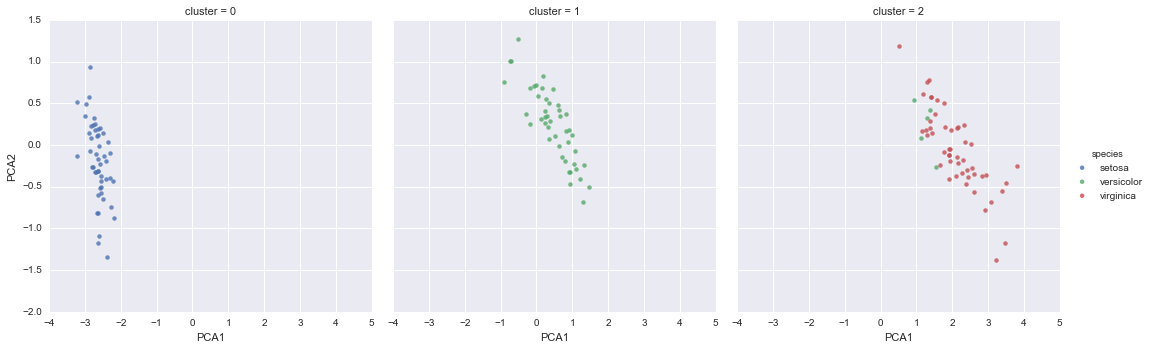
Bằng cách phân chia dữ liệu theo số cụm, chúng ta thấy rõ hơn cách thuật toán GMM đã khôi phục lại nhãn cơ bản: loại động vật setosa được tách biệt hoàn hảo trong cụm 0, trong khi vẫn tồn tại một lượng nhỏ sự kết hợp giữa các loại versicolor và virginica.Điều này có nghĩa rằng ngay cả khi không có một chuyên gia nào để chỉ cho chúng ta biết nhãn loại của các bông hoa cụ thể, đo đạc của những bông hoa này đủ đặc biệt để chúng ta có thể tự động xác định sự hiện diện của các nhóm loại khác nhau bằng một thuật toán gom cụm đơn giản!Cách thuật toán này có thể cung cấp những gợi ý cho các chuyên gia trong lĩnh vực về mối quan hệ giữa các mẫu mà họ đang quan sát.
Ứng dụng: Khám phá Chữ số viết tay¶
Để trình bày những nguyên tắc này trên một vấn đề thú vị hơn, chúng ta hãy xem xét một phần của vấn đề nhận dạng ký tự quang học: việc nhận dạng chữ số viết tay.Trong thực tế, vấn đề này bao gồm việc định vị và nhận dạng các ký tự trong một hình ảnh. Tuy nhiên, ở đây chúng ta sẽ lựa chọn một lối tắt và sử dụng tập dữ liệu các chữ số đã được định dạng trước của Scikit-Learn, điều này đã được tích hợp sẵn trong thư viện.
Tải và hiển thị dữ liệu chữ số
Chúng ta sẽ sử dụng giao diện truy cập dữ liệu của Scikit-Learn và xem xét dữ liệu này:
from sklearn.datasets import load_digitsdigits = load_digits()digits.images.shape
(1797, 8, 8)
Dữ liệu hình ảnh là một mảng ba chiều: 1,797 mẫu mỗi mẫu bao gồm một lưới 8 × 8 pixel.Hãy minh họa 100 mẫu đầu tiên này:
import matplotlib.pyplot as pltfig, axes = plt.subplots(10, 10, figsize=(8, 8), subplot_kw={'xticks':[], 'yticks':[]}, gridspec_kw=dict(hspace=0.1, wspace=0.1))for i, ax in enumerate(axes.flat): ax.imshow(digits.images[i], cmap='binary', interpolation='nearest') ax.text(0.05, 0.05, str(digits.target[i]), transform=ax.transAxes, color='green')

Để làm việc với dữ liệu này trong Scikit-Learn, chúng ta cần một biểu diễn hai chiều, [n_samples, n_features]. Chúng ta có thể thực hiện điều này bằng cách xử lý từng điểm ảnh trong hình ảnh như là một đặc trưng: tức là, bằng cách làm phẳng các mảng điểm ảnh để chúng ta có một mảng gồm 64 giá trị điểm ảnh đại diện cho mỗi chữ số.Ngoài ra, chúng ta cần mảng mục tiêu, cung cấp nhãn đã xác định trước cho mỗi chữ số.Hai đại lượng này được tích hợp trong tập dữ liệu số chữ viết tay dưới các thuộc tính data và target, tương ứng:
X = digits.dataX.shape
(1797, 64)
y = digits.targety.shape
(1797,)
Chúng ta thấy ở đây có 1.797 mẫu và 64 đặc trưng.
Học không giám sát: Giảm số chiều dữ liệu¶
Chúng tôi muốn hình dung các điểm của chúng tôi trong không gian tham số 64 chiều, nhưng rất khó để hiển thị các điểm một cách hiệu quả trong một không gian có số chiều cao như vậy.Thay vào đó, chúng tôi sẽ giảm số chiều xuống còn 2, bằng cách sử dụng một phương pháp không giám sát.Ở đây, chúng tôi sẽ sử dụng một thuật toán học manifold được gọi là Isomap (xem chi tiết tại Đặc trưng: Học Manifold), và chuyển đổi dữ liệu thành hai chiều:
from sklearn.manifold import Isomapiso = Isomap(n_components=2)iso.fit(digits.data)data_projected = iso.transform(digits.data)data_projected.shape
(1797, 2)
Chúng ta thấy rằng dữ liệu đã được dự đoán hiện tại là hai chiều.Hãy vẽ đồ thị của dữ liệu này để xem chúng ta có thể tìm hiểu được gì từ cấu trúc của nó:
plt.scatter(data_projected[:, 0], data_projected[:, 1], c=digits.target, edgecolor='none', alpha=0.5, cmap=plt.cm.get_cmap('spectral', 10))plt.colorbar(label='digit label', ticks=range(10))plt.clim(-0.5, 9.5);
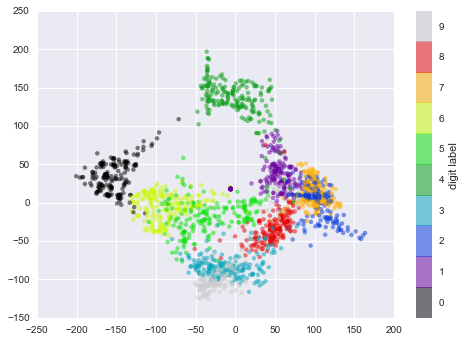
Biểu đồ này mang lại cho chúng ta một cái nhìn rõ ràng về việc các con số khác nhau được phân tách như thế nào trong không gian 64 chiều lớn hơn. Ví dụ, số không (trong màu đen) và số một (trong màu tím) gần như không có điểm chồng chéo trong không gian tham số.Một cách trực quan, điều này có ý nghĩa: số không rỗng ở giữa hình ảnh, trong khi số một thường có mực viết ở giữa.Mặt khác, dường như có một mạng lưới liền mạch hơn giữa số một và số bốn: chúng ta có thể hiểu điều này bằng cách nhận ra rằng một số người vẽ số một với “mũ” trên đầu, khiến chúng trông giống như số bốn.
Nhìn chung, tuy nhiên, các nhóm khác nhau dường như được tách biệt khá tốt trong không gian tham số: điều này cho chúng ta biết rằng một thuật toán phân loại giám sát rất đơn giản nên thực hiện phù hợp trên dữ liệu này.Hãy thử xem sao.
Phân loại chữ số¶
Hãy áp dụng một thuật toán phân loại vào các chữ số.Giống như dữ liệu Iris trước đây, chúng ta sẽ chia dữ liệu thành tập huấn luyện và tập kiểm tra, và phù hợp với một mô hình naive Bayes Gaussian:
Xtrain, Xtest, ytrain, ytest = train_test_split(X, y, random_state=0)
from sklearn.naive_bayes import GaussianNBmodel = GaussianNB()model.fit(Xtrain, ytrain)y_model = model.predict(Xtest)
Bây giờ khi chúng ta đã dự đoán được mô hình của chúng ta, chúng ta có thể đánh giá độ chính xác bằng cách so sánh các giá trị thực tế của bộ dữ liệu kiểm tra với các dự đoán:
from sklearn.metrics import accuracy_scoreaccuracy_score(ytest, y_model)
0.83333333333333337
Với cả mô hình rất đơn giản này, chúng ta thu được độ chính xác khoảng 80% cho việc phân loại các chữ số!Tuy nhiên, con số duy nhất này không cho chúng ta biết chính xác chúng ta đã làm sai ở đâu – một cách tốt để làm điều này là sử dụng ma trận nhầm lẫn, mà chúng ta có thể tính toán bằng Scikit-Learn và vẽ đồ thị bằng Seaborn:
from sklearn.metrics import confusion_matrixmat = confusion_matrix(ytest, y_model)sns.heatmap(mat, square=True, annot=True, cbar=False)plt.xlabel('predicted value')plt.ylabel('true value');
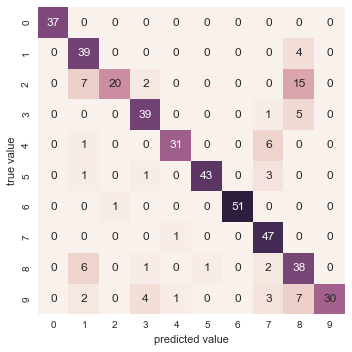
Đoạn mã trên cho chúng ta biết điểm bị nhãn sai thường xuất hiện ở đâu: ví dụ, có nhiều số hai ở đây bị phân loại sai bằng cách đánh dấu là số một hoặc số tám.Một cách khác để có hiểu biết về các đặc điểm của mô hình là vẽ lại các đầu vào, kèm theo nhãn dự đoán.Chúng ta sử dụng màu xanh lá cây cho các nhãn đúng và màu đỏ cho các nhãn sai:
fig, axes = plt.subplots(10, 10, figsize=(8, 8), subplot_kw={'xticks':[], 'yticks':[]}, gridspec_kw=dict(hspace=0.1, wspace=0.1))test_images = Xtest.reshape(-1, 8, 8)for i, ax in enumerate(axes.flat): ax.imshow(test_images[i], cmap='binary', interpolation='nearest') ax.text(0.05, 0.05, str(y_model[i]), transform=ax.transAxes, color='green' if (ytest[i] == y_model[i]) else 'red')

Khám phá phần nhỏ dữ liệu này, chúng ta có thể hiểu được vị trí mà thuật toán có thể không hoạt động tối ưu.Để vượt xa tỷ lệ phân loại 80% của chúng ta, chúng ta có thể chuyển sang một thuật toán phức tạp hơn như máy vector hỗ trợ (xem Sâu hơn: Máy vector hỗ trợ), rừng ngẫu nhiên (xem Sâu hơn: Cây quyết định và Rừng ngẫu nhiên) hoặc phương pháp phân loại khác.
Tóm tắt¶
Ở phần này, chúng ta đã trình bày các tính năng cơ bản của cách biểu diễn dữ liệu trong Scikit-Learn, và API của bộ ước lượng.Dù là loại ước lượng nào, thì cũng tuân theo cùng một mẫu “import/khởi tạo/fit/dự đoán”.Với thông tin về API của bộ ước lượng này, bạn có thể tham khảo tài liệu của Scikit-Learn và bắt đầu thử nghiệm các mô hình khác nhau trên dữ liệu của mình.
Trong phần tiếp theo, chúng ta sẽ tìm hiểu về có lẽ là chủ đề quan trọng nhất trong machine learning: cách lựa chọn và xác thực mô hình của bạn.









