Ba điểm và đường thẳng trong 3 chiều¶
Đồ thị ba chiều cơ bản nhất là đồ thị một đường hoặc tập hợp của các điểm quỹ đạo được tạo từ các bộ giá trị (x, y, z). Analog với các đồ thị hai chiều phổ biến hơn đã được thảo luận trước đây, các đồ thị này có thể được tạo bằng cách sử dụng các hàm ax.plot3D và ax.scatter3D.Chữ ký gọi cho chúng gần như giống như các đồng nghĩa hai chiều của chúng, vì vậy bạn có thể tham khảo Đồ thị Đường đơn giản và Đồ thị Phân tán đơn giản để biết thêm thông tin về kiểm soát đầu ra.Ở đây, chúng tôi sẽ vẽ một vòng xoắn học trí và một số điểm được vẽ ngẫu nhiên gần đường:
ax = plt.axes(projection='3d')# Data for a three-dimensional linezline = np.linspace(0, 15, 1000)xline = np.sin(zline)yline = np.cos(zline)ax.plot3D(xline, yline, zline, 'gray')# Data for three-dimensional scattered pointszdata = 15 * np.random.random(100)xdata = np.sin(zdata) + 0.1 * np.random.randn(100)ydata = np.cos(zdata) + 0.1 * np.random.randn(100)ax.scatter3D(xdata, ydata, zdata, c=zdata, cmap='Greens');
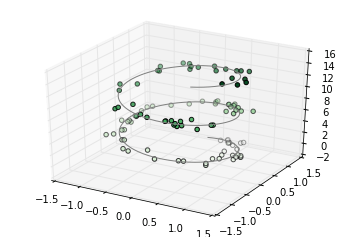
Lưu ý rằng mặc định, các điểm sự phân tán được điều chỉnh độ trong suốt để tạo cảm giác sâu sắc trên trang web.Mặc dù hiệu ứng ba chiều đôi khi khó nhìn thấy trên hình tĩnh, nhưng xem một cách tương tác có thể giúp bạn có được nhận thức tốt về cách bố trí các điểm.
Đồ thị đường đồng mức ba chiều
Tương tự như các đồ thị đường mức chúng ta đã khám phá trong Các Đồ Thị Mật Độ và Đường Mức, mplot3d có các công cụ để tạo ra các đồ thị đường mức ba chiều sử dụng cùng đầu vào.Giống như đồ thị hai chiều ax.contour, ax.contour3D yêu cầu tất cả dữ liệu đầu vào được biểu diễn dưới dạng các lưới hai chiều đều đặn, với dữ liệu Z được đánh giá tại mỗi điểm.Ở đây chúng tôi sẽ hiển thị một biểu đồ đường mức ba chiều của một hàm sin ba chiều:
def f(x, y): return np.sin(np.sqrt(x ** 2 + y ** 2))x = np.linspace(-6, 6, 30)y = np.linspace(-6, 6, 30)X, Y = np.meshgrid(x, y)Z = f(X, Y)
fig = plt.figure()ax = plt.axes(projection='3d')ax.contour3D(X, Y, Z, 50, cmap='binary')ax.set_xlabel('x')ax.set_ylabel('y')ax.set_zlabel('z');

Đôi khi góc nhìn mặc định không phải là tối ưu, trong trường hợp này chúng ta có thể sử dụng phương thức view_init để thiết lập góc nghiêng và góc phương đồ. Trong ví dụ sau đây, chúng ta sẽ sử dụng góc nghiêng là 60 độ (tức là 60 độ phía trên mặt phẳng x-y) và góc phương đồ là 35 độ (tức là xoay ngược chiều kim đồng hồ 35 độ xung quanh trục z):
ax.view_init(60, 35)fig
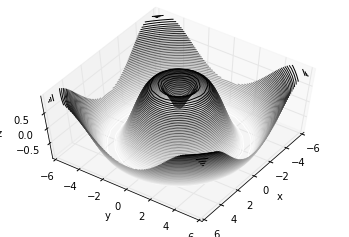
Một lần nữa, hãy chú ý rằng việc xoay này có thể thực hiện được một cách tương tác bằng cách nhấp và kéo khi sử dụng một trong những giao diện người dùng tương tác của Matplotlib.
Các Mô Hình Dây Chuyền và Biểu Đồ Bề Mặt¶
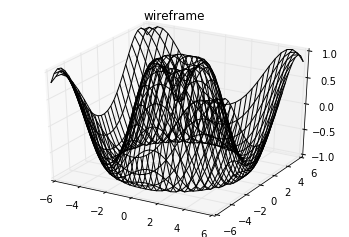
Hai loại biểu đồ ba chiều khác dành cho dữ liệu lưới là biểu đồ dây và biểu đồ bề mặt. Chúng lấy một lưới giá trị và chiếu lên bề mặt ba chiều được chỉ định, và có thể giúp dễ dàng hình dung các hình dạng ba chiều kết quả. Đây là một ví dụ về việc sử dụng biểu đồ dây:
fig = plt.figure()ax = plt.axes(projection='3d')ax.plot_wireframe(X, Y, Z, color='black')ax.set_title('wireframe');
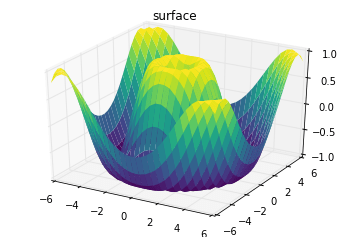
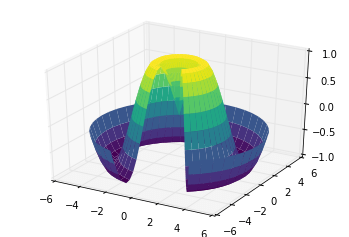
Một đồ thị bề mặt tương tự như một đồ thị dây, nhưng mỗi mặt của đồ thị dây là một đa giác được tô màu.Thêm một bảng màu vào các đa giác tô màu có thể giúp nắm bắt được hình dạng của bề mặt được trực quan hóa:
ax = plt.axes(projection='3d')ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='viridis', edgecolor='none')ax.set_title('surface');
Lưu ý rằng mặc dù lưới giá trị cho một biểu đồ bề mặt cần phải là hai chiều, nhưng không nhất thiết phải là chữ nhật.
r = np.linspace(0, 6, 20)theta = np.linspace(-0.9 * np.pi, 0.8 * np.pi, 40)r, theta = np.meshgrid(r, theta)X = r * np.sin(theta)Y = r * np.cos(theta)Z = f(X, Y)ax = plt.axes(projection='3d')ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='viridis', edgecolor='none');
Surface Triangulations¶
Đối với một số ứng dụng, các lưới được lấy mẫu đều bắt buộc bởi các phương pháp trên là quá hạn chế và bất tiện.Trong những tình huống này, các biểu đồ dựa trên xác định tam giác có thể rất hữu ích.Còn nếu thay vì lấy mẫu đều từ một lưới Descartes hoặc cực, chúng ta có thay thế bằng một tập hợp các lựa chọn ngẫu nhiên?
theta = 2 * np.pi * np.random.random(1000)r = 6 * np.random.random(1000)x = np.ravel(r * np.sin(theta))y = np.ravel(r * np.cos(theta))z = f(x, y)
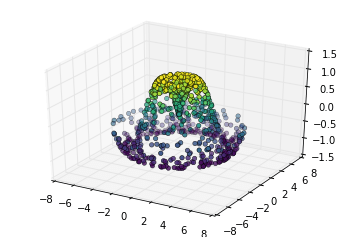
Chúng ta có thể tạo ra một biểu đồ phân tán của các điểm để có được một ý tưởng về bề mặt mà chúng ta đang lấy mẫu từ:
ax = plt.axes(projection='3d')ax.scatter(x, y, z, c=z, cmap='viridis', linewidth=0.5);
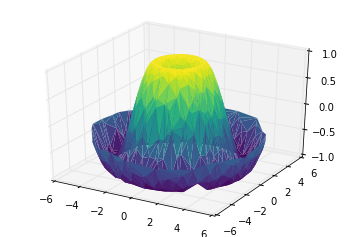
Điều này để lại rất nhiều điều cần yêu cầu.Chức năng sẽ giúp chúng ta trong trường hợp này là ax.plot_trisurf, tạo ra một bề mặt bằng cách tìm một tập hợp các tam giác được tạo ra giữa các điểm kề nhau (lưu ý rằng x, y và z ở đây là các mảng một chiều):
ax = plt.axes(projection='3d')ax.plot_trisurf(x, y, z, cmap='viridis', edgecolor='none');
Kết quả nhất định không sạch sẽ như khi vẽ bằng lưới, nhưng tính linh hoạt của một sự ba lần như vậy cho phép vẽ một số đồ thị ba chiều thực sự thú vị. Ví dụ, thực ra có thể vẽ một đường cong Möbius ba chiều bằng cách này, như chúng ta sẽ thấy trong phần tiếp theo.
Ví dụ: Hình dung một vòng Mobius¶
Một vòng Möbius tương tự như một dải giấy được dán thành một vòng với một nửa xoắn.Theo mặt địa lý, nó rất thú vị vì mặc dù có vẻ như nó chỉ có một mặt duy nhất!Ở đây, chúng ta sẽ trực quan hóa một đối tượng như vậy bằng cách sử dụng công cụ ba chiều của Matplotlib.Chìa khóa để tạo ra vòng Möbius là nghĩ về cách tham số hóa của nó: nó là một dải hai chiều, vì vậy chúng ta cần hai chiều nội tại. Hãy gọi chúng là $\theta$, có giá trị từ $0$ đến $2\pi$ xung quanh vòng, và $w$ có giá trị từ -1 đến 1 theo chiều rộng của dải:
theta = np.linspace(0, 2 * np.pi, 30)w = np.linspace(-0.25, 0.25, 8)w, theta = np.meshgrid(w, theta)
Bây giờ từ phép điều chỉnh này, chúng ta phải xác định các vị trí (x, y, z) của dải nhúng.
Suy nghĩ về điều đó, chúng ta có thể nhận ra rằng có hai phép xoay xảy ra: một là vị trí của vòng lặp xung quanh trung tâm của nó (chúng ta gọi là $\theta$), trong khi phép xoắn của dải xung quanh trục của nó (chúng ta sẽ gọi là $\phi$). Đối với một dải Möbius, chúng ta phải có dải thực hiện một nửa phép xoắn trong một vòng lặp đầy đủ, hoặc $\Delta\phi = \Delta\theta/2$.
phi = 0.5 * theta
Bây giờ chúng ta sử dụng kiến thức về hình học tam giác để tạo ra một nhúng ba chiều.Chúng ta sẽ định nghĩa $r$, khoảng cách từ mỗi điểm đến trung tâm, và sử dụng điều này để tìm tọa độ nhúng $(x, y, z)$:
# radius in x-y planer = 1 + w * np.cos(phi)x = np.ravel(r * np.cos(theta))y = np.ravel(r * np.sin(theta))z = np.ravel(w * np.sin(phi))
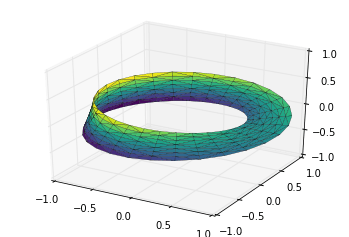
Kết thúc, để vẽ đối tượng, chúng ta phải đảm bảo rằng sự ba chúc đã đúng. Cách tốt nhất để làm điều này là xác định sự ba chúc trong mô tả parametri cơ bản, sau đó cho phép Matplotlib chuyển đổi sự ba chúc này vào không gian ba chiều của dải Möbius.Điều này có thể được thực hiện như sau:
# triangulate in the underlying parametrizationfrom matplotlib.tri import Triangulationtri = Triangulation(np.ravel(w), np.ravel(theta))ax = plt.axes(projection='3d')ax.plot_trisurf(x, y, z, triangles=tri.triangles, cmap='viridis', linewidths=0.2);ax.set_xlim(-1, 1); ax.set_ylim(-1, 1); ax.set_zlim(-1, 1);
Kết hợp tất cả các kỹ thuật này, ta có thể tạo và hiển thị một loạt các đối tượng và mẫu ba chiều khác nhau trong Matplotlib.










